Recognize a context free language
Given the grammar of a context free language and a string, decide if the string can be generated by the grammar.
In general, the syntax tree generating the given string is requested, but for simplification we omit this part in this note.
Context free grammar
The grammar of a context free language consists of a start symbol, and some rewriting rules, as in the following example. Left hand sides consists of symbols, called non terminals, and the right hand side of a string mixing non terminals and terminals (which are the symbols from the strings we wish to recognize). Often we use upper case letters for non terminals and lower case letters for terminals.
The following example describes all palindromes on the letter a, b.
S -> a S a
S -> b S b
S -> b
S -> a
S ->
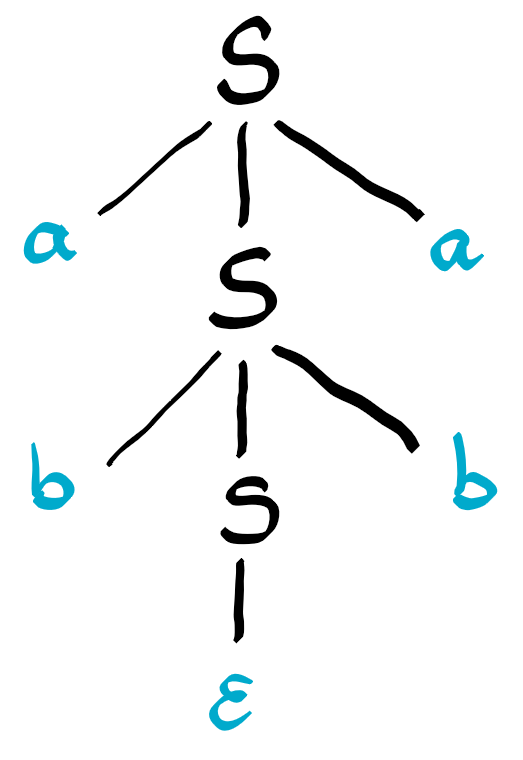
For example the palindrome abba can be generated from the start symbol S, using the following replacements S -> a S a -> a b S b a -> a b b a (see figure below). The last step, uses the last rule, were S can be replaced by the empty string, denoted by $\epsilon$ in the figure.
We observe that context free languages form a larger class than regular languages. If you want to recognize palindromes with a finite state automaton, you would need to memorize the prefix seen so far, to compare it with the suffix, and with only a finite number of states, there is not enough memory for this task.
Representation in Python
We will encode a grammar using a Python class. The start symbol is called start. Rules are stored in a list called rules, consisting of pairs composed of the left and the right hand side. The right hand side is simply a list. For convenience we maintain a set of all the non terminals, and call it nonterm. It is assumed that all non terminals appear at the left hand side of some rule.
class ContextFreeGrammar:
def __init__(self, start):
self.start = start
self.rules = []
self.nonterm = set()
def add_rule(self, left, right):
# need to transform string into list, for normalization will manipulate them
self.rules.append((left, list(right)))
self.nonterm.add(left)
Chomsky normal form
One method to recognize if a string is recognized by a context free grammar, is to first normalize the grammar. The goal is to end up in an equivalent grammar, where every rule is in one of the following forms.
A -> B C # right hand side contains exactly two non terminals and none of them is the start symbol
A -> a # right hand side contains exactly one terminal
S -> # only the start symbol might generate the empty string
The normalization is done by a sequence of steps, called START, TERM, BIN, DEL and UNIT. They should be applied in a specific order, such that the grammar size increases only quadratically.
Start symbol
First we want to have a start symbol which does not appear in the right hand side of any rule. Well we simply introduce a new symbol S0, which will be the new start symbol, together with a single rule S0->S where S is the original start symbol.
Note that we need a method generating new start symbols. Which we implemented quite roughly, assuming that no non-terminal is of the form Ni for some number i. A safer choice could be to use _ instead of N.
def new_symbol(self):
"""returns a new unused non terminal.
Risky unchecked assumption: existing non terminals are not of the form N1234.
"""
return "N{}".format(len(self.nonterm))
def norm_start(self):
S0 = self.new_symbol()
self.add_rule(S0, [self.start])
self.start = S0
Introduce a dedicated non terminal for every terminal
For every rule with more than one symbol on the right hand side, we want it to consist only of non terminals. For this purpose, we introduce a dedicated non terminal for every terminal. The dictionary term keeps track of these new symbols.
Note that in this code we modify the right hand side of some rules, this motivates the use of lists, instead of strings or tuples, which are not mutable.
def norm_term(self):
term = {}
for left, right in self.rules:
if len(right) >= 2: # only non singleton rules
for i, x in enumerate(right):
if x not in self.nonterm: # x is terminal
if x not in term:
term[x] = self.new_symbol()
self.add_rule(term[x], [x])
right[i] = term[x] # replace by corresponding non terminal
Restrict right hand sides to pairs
Now we want to get rid of long sequences in the right hand side. Again for this we need to introduce new symbols. For example
A -> B C D E F
will be replaced by
N1 -> B C
N2 -> N1 D
N3 -> N2 E
A -> N3 F
The rewriting is done by iterative pairing, the first pair consists of the first two elements of the right hand side, while the subsequent pairs consist of the symbol representing the last pair, followed by the next symbol of the right hand side. Note how we deal with the special case of the first pair, by using a variable called last.
def norm_bin(self):
for i, left_right in enumerate(self.rules):
left, right = left_right
if len(right) > 2:
last = right[0] # last introduced non terminal, except first rule
for j in range(1, len(right) - 1):
pair = self.new_symbol()
self.add_rule(pair, [last, right[j]])
last = pair
self.rules[i] = (left, [last, right[-1]])
Removing rules producing the empty string
Next step is to remove all rules producing the empty string, except possibly for the start symbol. The idea is to first detect which symbols N can generate the empty string. It might be because there is a rule of the form N -> emptystring or N -> A and A can generate the empty string. We call such symbols nullable. These symbols could be identified using a priority queue, counting how many nullable elements a rule has in its right hand side, and using an inverse reference, mapping symbols to all rules where they appear in the right hand side. For simplicity we follow a brute force approach, stopping when a fixpoint is reached.
Then for each rule of the form A -> B C, if B is nullable, we introduce the rule A -> C. We proceed similar in case C is nullable. In addition we remove all rules generating the empty string, except for the start symbol.
def norm_del(self):
# detect nullable non terminals in brute force manner
nullable = set()
before = -1 # arbitrary number to initiate the loop
while len(nullable) != before: # until fixpoint reached
before = len(nullable)
for left, right in self.rules:
if all(x in nullable for x in right):
nullable.add(left)
for left, right in self.rules:
if len(right) == 2: # assume method is called after norm_bin
if right[0] in nullable:
self.add_rule(left, [right[1]])
if right[1] in nullable:
self.add_rule(left, [right[0]])
# now remove all rules of the form N -> empty
self.rules = [(left, right) for left, right in self.rules if len(right) > 0]
if self.start in nullable:
self.add_rule(self.start, []) # except for start symbol
Remove rules with a unique non terminal on the right hand side
The last step, which seems to be hardest, is to remove all rules of the form A -> B. These are called unit rules. For this we consider the directed graph where each rule of the form A -> B generates a corresponding arc. We store this graph in mappings arc_in and arc_out which associate to a non terminal B the set of all non terminals with arcs pointing inwards to B or outwards from B.
The set gen_in will eventually become the transitive closure of the incoming arcs, i.e. gen_in[D] contains all symbols A that lead to D through a sequence of arcs A->B->C->D for example. For this we explore the graph in topological order, where we need the crucial assumption that there are no circular unit rules in the grammar. The exploration starts with a vertex of zero indegree, and removes himself from the graph. Every vertex that has now zero indegree joins the queue Q of vertices, which are ready to be processed.
Finally every rule of the form B -> RHS generates a rule A -> RHS for every symbol A in gen_in[B], i.e. which can be rewritten as B.
def is_unit(self, right): return len(right) == 1 and right[0] in self.nonterm
def norm_unit(self):
# we assume that there are no circular unit rules such as A -> B, B -> A
arc_out = defaultdict(set) # arc_out[A] is set of all B with A->B
arc_in = defaultdict(set) # arc_in[B] is set of all A with A->B
gen_in = defaultdict(set) # gen_in[D] is set of all A with A->B->...->D
# build those from unit rules
for left, right in self.rules:
if self.is_unit(right):
arc_out[left].add(right[0])
arc_in[right[0]].add(left)
# remove unit rules
self.rules = [(left, right) for left, right in self.rules if not self.is_unit(right)]
# process in topological order
Q = [u for u in arc_out if len(arc_in[u]) == 0]
while Q:
u = Q.pop()
for v in arc_out[u]:
gen_in[v] |= gen_in[u]
gen_in[v].add(u)
arc_in[v].remove(u)
if len(arc_in[v]) == 0:
Q.append(v)
# add new rules
for left, right in self.rules:
for v in gen_in[left]:
self.add_rule(v, right)
In action on the palindrome example
We start with the above mentioned grammar.
start symbol S
S -> a S a
S -> b S b
S -> b
S -> a
S ->
After the START step we obtain:
start symbol N1
S -> a S a
S -> b S b
S -> a
S -> b
S ->
N1 -> S
After the TERM step we obtain:
S -> N2 S N2
S -> N3 S N3
S -> a
S -> b
S ->
N1 -> S
N2 -> a
N3 -> b
After the BIN step we obtain:
S -> N4 N2
S -> N5 N3
S -> a
S -> b
S ->
N1 -> S
N2 -> a
N3 -> b
N4 -> N2 S
N5 -> N3 S
After the DEL step we obtain:
S -> N4 N2
S -> N5 N3
S -> a
S -> b
N1 -> S
N2 -> a
N3 -> b
N4 -> N2 S
N5 -> N3 S
N4 -> N2
N5 -> N3
N1 ->
After the UNIT step we obtain:
S -> N4 N2
S -> N5 N3
S -> a
S -> b
N2 -> a
N3 -> b
N4 -> N2 S
N5 -> N3 S
N1 ->
N1 -> N4 N2
N1 -> N5 N3
N1 -> a
N1 -> b
N4 -> a
N5 -> b
The Cocke-Younger-Kasami algorithm
The Cocke-Younger-Kasami Algorithm solves the string recognition problem using dynamic programming. It assumes that the given grammar is in Chomsky norm form. If s is the string of length n, then P[i,j] is a table storing the set of non terminals generating the substring s[i:j+1]. So the string is recognized by the grammar if and only if the start symbol belongs to P[0, n-1].
The base case concerns all individual characters in s. Namely P[i,i] is the set of all nonterminals generating the i-th character of s.
The induction case, concerns all larger substrings. In order to compute P[i,j], we consider all possibilities to split [i,j] into [i,k] and [k+1,j]. Then for each rule of the form A -> B C, if B belongs to P[i,k] and C belongs to P[k+1,j], then A can be added to P[i,j].
The complexity is O(n^3 k), where n is the size of the given string n and k the size of the grammar (the number of rules), which its self can be quadratic in the size of the original grammar (not yet in Chomsky normal form), and here the size is the number of plus plus the total length over all right hand sides.
def cocke_younger_kasami(self, s):
"""" returns a list of all pairs (i,j) such that
s[i:j] is generated by the grammar
"""
self.normalize()
N = range(len(s))
best = None
# P[i][j] is the set of all non terminals generating s[i:j+1]
P = [[set() for j in N] for i in N]
# base case
for i in N:
for left, right in self.rules:
if right == [s[i]]:
P[i][i].add(left)
# induction
for j in N:
for i in range(j - 1, -1, -1): # order is important
for k in range(i, j):
for left, right in self.rules:
if len(right) == 2 and right[0] in P[i][k] and right[1] in P[k+1][j]:
P[i][j].add(left)
answer = []
for j in N:
for i in range(j + 1):
if self.start in P[i][j]:
answer.append((i, j + 1)) # +1, because j + 1 is excluded
return answer