Determine the fixpoint of a rewriting system
Given the a rewriting system of the form $f:\Sigma\rightarrow \Sigma^\star$, determine the limit of $f^i(a)$ for some given seed letter $a\in \Sigma$.
Rewriting system
Consider the infinite sequence $a,f(a),f(f(a)),\ldots$. In the first step, letter $a$ is replaced by the string $f(a)$. In the second step every letter in $f(a)$ is replaced by its image by $f$ and the results are concatenated, and so on.
Consider these examples:
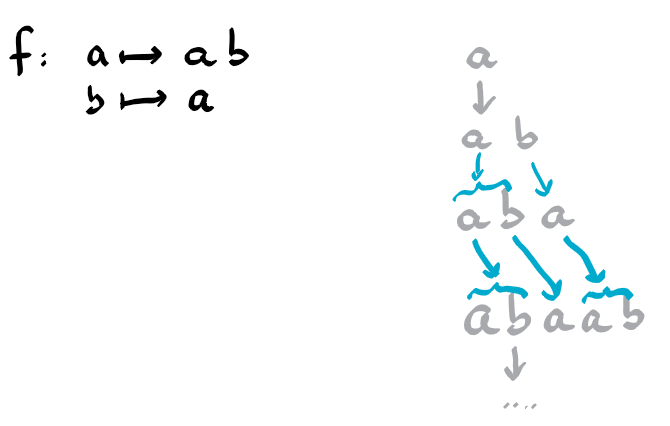
- $f:\: a \mapsto bb,\: b \mapsto b$
- a, bb, bb, bb, …
- $f:\: a \mapsto ab,\: b \mapsto a$
- a, ab, aba, abaab, abaab, abaababa, abaababaabaab, …
- $f:\: a \mapsto ba,\: b \mapsto c,\: c \mapsto b$
- a, ba, cba, bcba, cbcba, bcbcba, …
We can observe quite different behaviors. The first example reaches quickly a fixpoint, the second example seems to converge to a fixpoint (in form of an infinite string), but which is not reached within a finite number of steps. And the last example observes some cyclic behavior.
Letter type
This motivates us to distinguish 3 types of letters, depending on properties of the sequence generated by sucessive applications of $f$ starting with the letter $x$.
- Letter $x$ is of type 1 if successive applications of f eventually reach a fixpoint, i.e. if there is an integer i such that $f^i(a)=f^{i+1}(a)$.
- Letter $x$ is of type 2 if for every integer k there is an integer i such that $f^i(x)$ has length at least k and the k first letters are the same in all strings $f^j(x)$ for $j\geq i$.
- Letter $x$ is of type 0 in the remaining case.
Notation
We denote the i-th string in this sequence by $f^i(a)$. If the sequence has a limit, then denote it by $f^\star(a)$. In particular if $f^\star(a)$ is a finite string, then it is reached in a finite number of iterations, and $a$ is of type 2. If $f^\star(a)$ is an infinite string, then clearly it is not reached within a finite number of steps, and $a$ is of type 2. (This is less obvious, but I believe it to hold.)
Simplification
We might get rid of letters $x$ which are mapped to the empty string, simply by removing $x$ from all right handsides. This can be done with a queue containing symbols to be removed, and whenever the right hand side of some rule becomes empty, the left hand side enters the queue.
From now on, let’s assume that $f$ does not map to an empty string for all letters considered in the problem.
Rules determining the types
Basic rules:
- If $f(x)=x$, then $x$ has type 1. ($x$ is a fixpoint for $f$)
-
If $f(x)=xw$ for some arbitrary non empty word $w$, then $x$ is of type 2. Indeed, it generates the sequence $x, xw, xwf(w), xwf(w)f(f(w)), \ldots$.
- If $f(x)=y$ for some letter $y\neq x$, then clearly $x$ has the same type as $y$. But if these implications are circular, then $x$ has type 0 (and so have y and all the other letters along the cycle).
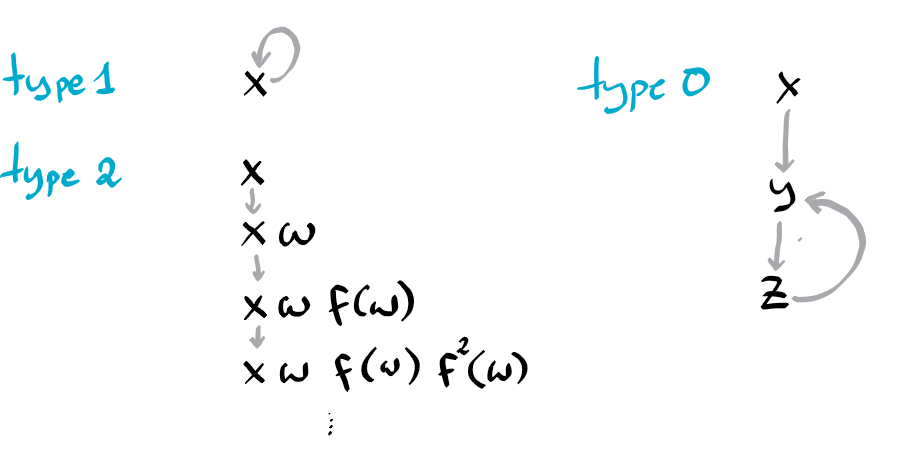
More complex rules:
If $f(x) = y_1 y_2 \ldots y_k$ with $y_1 \neq x$ and $k > 1$, then things become more interesting.
If all letters $y_1 y_2 \ldots y_k$ are of type 1, then so is $x$. Simply because the limit of f on x is $f^\star(y_1\ldots y_k)$ which is $f^\star(y_1)\ldots f^\star(y_k)$.
If $y_i$ is the first letter not of type 1, then the type of x is determined by the type of $y_i$. Again if this leads to a circular dependecy – for example when $y_i=x$ – then $x$ has type 2. Indeed in the limit f will generate on x the string $w^\star$, where $w$ is the fixpoint reached by $y_1,\ldots,y_{i-1}$.
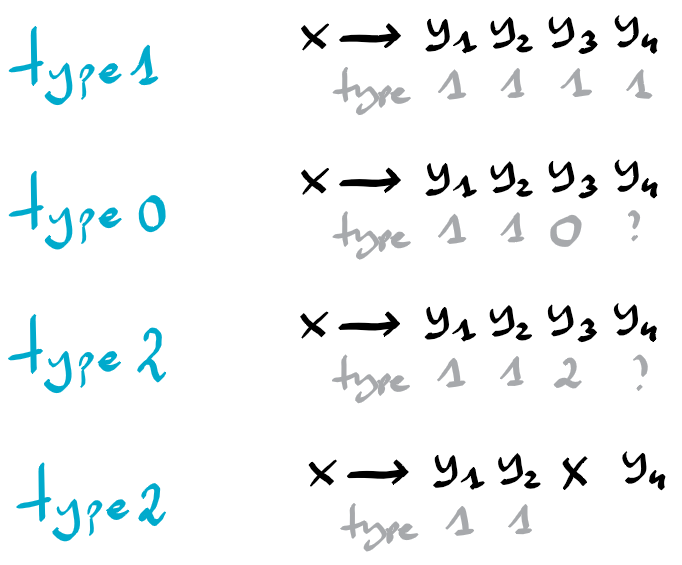
How to determine efficiently the types?
We will maintain a table type indexed by the alphabet. Initially all letters have an unknown type, that we could represent by the constant -1. For an implementation in Python, one would like to name the table kind instead to avoid the use of a keyword.
First we apply the basic rules, by setting the type of all letters $x$ with $f(x)=x$ or $f(x)=xw$.
Then for the remaining letters we inspect a function $g$, mapping $x$ to the first letter of $f(x)$. If iterated mapping of $g$ on a letter, ends on a letter with a defined type, then we don’t do anything for the moment. But if it ends on a cycle composed of letters with undefined type, then we know that all letters covered by the cycle need to be set to type 0.
Next, for all letters $x$ of undefined type, we maintain a pointer pos[x] on the string $f(x)$, such that we already know that all letters before this position have type 1. If the letter pointed by pos[x] has type 1, then clearly we can increment pos[x]. But if it has type is 0 or 2, then the type of $x$ must become the same type (0 or 2). If all letters of $f(x)$ have type 1 (pos[x] exceeds the length of $f(x)$), then the type of $x$ is set to $1$.
And finally we can safely set to 2 the type of all yet undefined letters.
Time complexity
It is $O(kn)$, where $k$ is the size of the alphabet and $m$ is the total length of the images of $f$, hence roughly the size of the input.
Implementation in C++
#include <iostream>
#include <map>
#include <vector>
#include <algorithm>
using namespace std;
int n;
vector<vector<int>> f;
bool solve(vector<vector<int>> &f) {
int n = f.size();
int kind[n]; // # -1 means undefined, 2 means infinity
int pos[n] = {0};
// pos[x] is index of first letter of f[x]s with still unknown type
fill(kind, kind + n, -1);
// start with obvious types (kinds)
for (int x = 0; x < n; x++) {
if (f[x][0] == x) {
if (f[x].size() == 1)
kind[x] = 1; // basic type 1 letter
else
kind[x] = 2; // basic type 2 letter
}
}
// obvious 0 types
for (int x = 0; x < n; x++) {
if (kind[x] == -1) { // for all yet undefined type letters
bool seen[n] = {false}; // trace of path
int y = x; // letter walking along path
while (!seen[y] && kind[y] == -1) { // stop at loop or at defined type letter
seen[y] = true;
y = f[y][0]; // next step in path (restrict f to first letter)
}
if (seen[y]) // path ended in a loop
for (int z = 0; z < n; z++)
if (seen[z])
kind[z] = 0; // whole path becomes type 0
}
}
// propage knowledge
// remaining letters x are of the form
// f[x] = y1 y2 ... yk for y1 != x and k>=1
bool changed = true;
while (changed) { // until fix point reached
changed = false;
// could use priority queue, but for 26 letters trying all is ok
for (int x = 0; x < n; x++) {
if (kind[x] == -1) { // need to learn type of x
if (pos[x] == f[x].size()) { // f maps x only to type 1 letters
kind[x] = 1; // hence x has type 1 as well
changed = true;
}
else if (kind[f[x][pos[x]]] == 1) { // additional type 1 letter in prefix
pos[x] += 1;
changed = true;
}
else if (kind[f[x][pos[x]]] != -1) {
kind[x] = kind[f[x][pos[x]]]; // inherit type
changed = true;
}
}
}
}
// default remaining type is 2
for (int x = 0; x < n; x++)
if (kind[x] == -1)
kind[x] = 2;
return kind[0] >= 1; // type of letter 'a'
}
int main(int argc, char const *argv[])
{
int t, n;
cin >> t; // number of testcases
while (t-->0) {
cin >> n;
vector<vector<int>> f;
while (n-->0) { // read mapping f
string s;
cin >> s;
vector<int> image;
for (char c: s) // convert string into int vector
image.push_back(c - 'a');
f.push_back(image);
}
if (solve(f))
cout << "YES" << endl;
else
cout << "NO" << endl;
}
}