Shortest path with negative edge weights
Given directed graph with possibly negative edge weights, find a shortest path between two given vertices.
(*) the above mentionned problem at SPOJ has invalid test data, and therefore as of today (January 2021) we cannot submit our solutions.
Distance
By length of a path we mean the total weight of the edges along the path. The distance between the source and a vertex v is defined as the length of a shortest path from the source to v. If v is not reachable from the source, by convention the distance is $+\infty$. And if for any arbitrary small length $\ell$ there is a path of length at most $\ell$, then by convention the distance is $=-\infty$.
The goal is to compute a distance vector such that $d^*[v]$ is the distance from the source to $v$.
Negative cycles
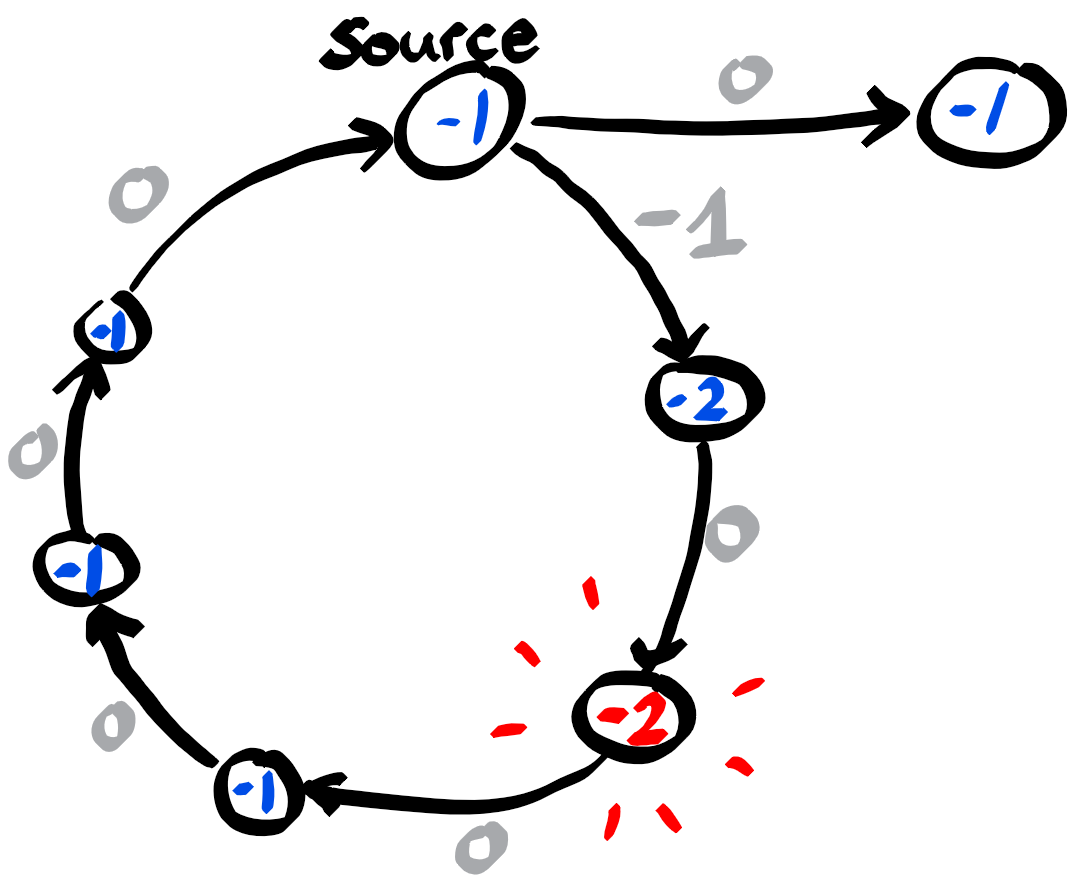
An important aspect of this problem are cycles of negative length. Namely, if there is a path from the source to $v$ with an intermediate vertex $u$, belonging to a negative cycle, then $d^*[v]=-\infty$, since one can loop an arbitrary number of times along the cycle, before reaching v.
Bellman-Ford
If the graph is sparse, then the algorithm of choice would be Bellman-Ford’s algorithm (also known as Bellman-Ford-Moore). It has complexity O(nm), where n is the number of vertices and m the number of arcs.
The algorithm works with a distance vector d upper bounding $d^*$, where d[v] represents the length of a known path from the source to v. Initially d contains only $+\infty$, except for the source, where the distance is 0 (the empty path). Then in every iteration, the distances in d are relaxed by updating for all arcs (u,v), $d[v] = d[u] + w[u,v]$, if $d[u]+w[u,v]$ is strictly smaller than the current distance $d[v]$.
This has to be done for $n-1$ iterations at most, and one can stop before if a fixpoint is reached (i.e. if $d$ did not change during one iteration). Simply because the $i$-th iteration computes the minimum among all paths consisting of at most $i$ arcs.
If finally we still have $d^+[v]=+\infty$, then $v$ is not reachable from the source.
Detecting negative cycles
If an n-th iteration still changes the vector $d$, then there are negative cycles, reachable from the source. Note that in the negative case, it is still possible that there are negative cycles which are not reachable from the source. If the goal is to detect these negative cycles as well, one could add a dummy source, connecting to all vertices with 0 weighted arcs.
If the graph is undirected, we can now set the distance $-\infty$ to all vertices reachable from the source, because it is now possible to reach the negative cycle from the source, loop any desired number of times, come back to the source and reach from there a target vertex.
However for directed graphs, we need to detect which are the vertices reachable from a negative cycle (itself reachable from the source). Since the distance decrease on the vertices propagate one arc every iteration along the graph, in the worst case we would need $n-1$ additional iterations to detect a distance decrease at the vertices v with $d^*[v]=-\infty$.
Implementation in Python
For vertices v with dist[v]=$-\infty$, when following the prec pointers, we find a path leading to a negative cycle and looping on this cycle.
def bellman_ford2(graph, weight, source):
""" Single source shortest paths by Bellman-Ford
:param graph: directed graph in listlist or listdict format
:param weight: can be negative.
in matrix format or same listdict graph
:returns: distance table, precedence table, bool
:explanation: bool is true if there is a negative cycle
reachable from the source.
distance[v] is +inf if vertex v is not reachable
from source and -inf if there are paths from the
source to v of arbitrary small weight.
:complexity: `O(|V|*|E|)`
"""
n = len(graph)
dist = [float('inf')] * n
prec = [None] * n
dist[source] = 0
def relax():
for nb_iterations in range(n-1):
for node in range(n):
for neighbor in graph[node]:
alt = dist[node] + weight[node][neighbor]
if alt < dist[neighbor]:
dist[neighbor] = alt
prec[neighbor] = node
relax()
intermediate = dist[:] # is fixpoint in absence of neg cycles
relax()
for node in range(n):
if dist[node] < intermediate[node]:
dist[node] = float('-inf')
return dist, prec, min(dist) == float('-inf')