Bipartite minimum vertex cover (alternative explanation)
Given an undirected bipartite graph find a minimum cardinality vertex set which covers all edges in the sense that it contains at least one endpoint of each edge.
Matching
This problem is deeply related to matching. So let’s review first some basic concepts of matching.
A matching is a collection of edges which are vertex disjoint. The goal is usually to find a matching of maximum cardinality. Vertices which are not adjacent to an edge of the matching are said to be free, otherwise they are matched.
Let’s build such a matching greedily on the following graph, adding arbitrary edges as long as it is possible.
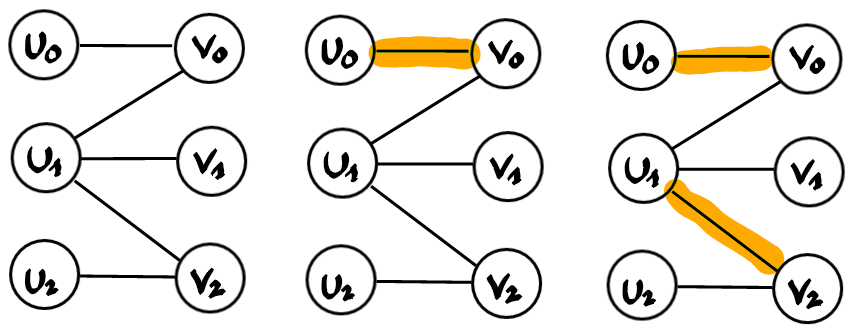
We are stuck with the right most matching which consists of 2 edges, while there is a perfect matching consisting of 3 edges. There is no way to add additional edges to the matching without removing some of them.
Let’s look at the symmetric difference between two matchings, the sub-optimal yellow one and the optimal blue one.
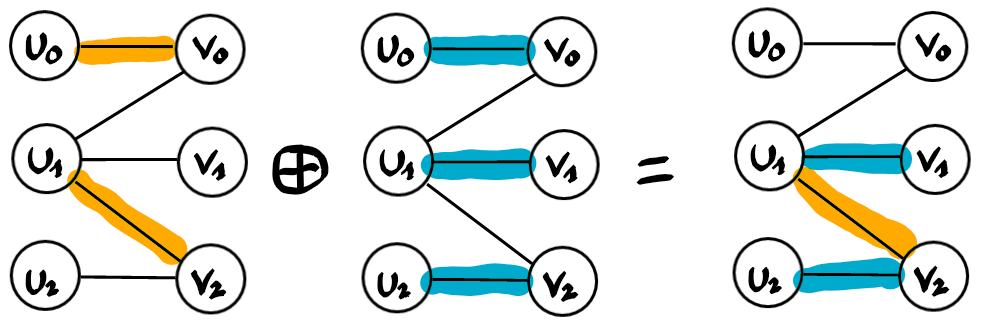
In general the result is a collection of cycles and paths, each alternating with edges from the yellow and edge from the blue matching. In this example there is a single path, namely u2-v2-u1-v1. We observe that the two endpoints of the path are free for the yellow matching. Such a path is called an alternating augmenting path. Why augmenting? Because if we take the symmetric difference between the yellow matching and this path, then we obtain the blue matching. The cardinality increased by exactly one during the process, namely the endpoints of the path are now matched, all inner vertex of the path remain matched, just to different vertices.
This shows that one can find a maximum cardinality matching iteratively by finding augmenting alternating paths and using them to increase the current matching. This is a sort of greedy algorithm, just that we don’t add edges greedily but augmenting paths.
The main difficulty is then to find augmenting paths, but for bipartite graphs this can be done by a simple graph exploration. Start with a free vertex on the left say, let it be the root, and build an alternating exploration tree. By alternating we mean that every path from the root to some leaf alternates between edges not in the current matching and edges in the current matching.
If one of the leafs is a free vertex, then we found our augmenting path, namely the path from the root to this leaf. If the tree cannot be extended anymore, but contains only matched leafs (which must be on the same side as the root in this bipartite graph), then we have the proof that the matching is maximum.
Here you can see an implementation of this algorithm.
Relation with Vertex Cover
Now we have two optimization problems. Vertex Cover asks for a smallest vertex set while matching asks for a largest edge set. It happens that these problems are so strongly related, that the optimum solutions to both problems have the same cardinality. The proof is constructive and hence provides an algorithm to build a minimum vertex cover from a maximum matching.
To be a bit more formal, let’s introduce some notation. G(U,V,E) is the bipartite graph. M a maximum matching and S a vertex cover.
S covers all edges, in particular the edges of the matching M. But every vertex of S can cover at most one edge of M. Therefore $|S| \geq |M|$.
Now we define a set Z as follows. It contains all free vertices from U, and all vertices reachable from them by alternating paths. Z partitions the vertices into four parts, namely
- $U\setminus Z$
- $U\cap Z$
- $V\setminus Z$
- $V\cap Z$.
If we were (unsuccessfully) trying to augment the matching M, then the alternating trees we build for this purpose cover exactly Z. By maximality of M there is no edge from $U \cap Z$ to $V\setminus Z$. Also by maximality of Z all matching edges have either both endpoints in Z or none.
In the following picture vertices in Z are shown in gray. Solid edges constitute the matching.
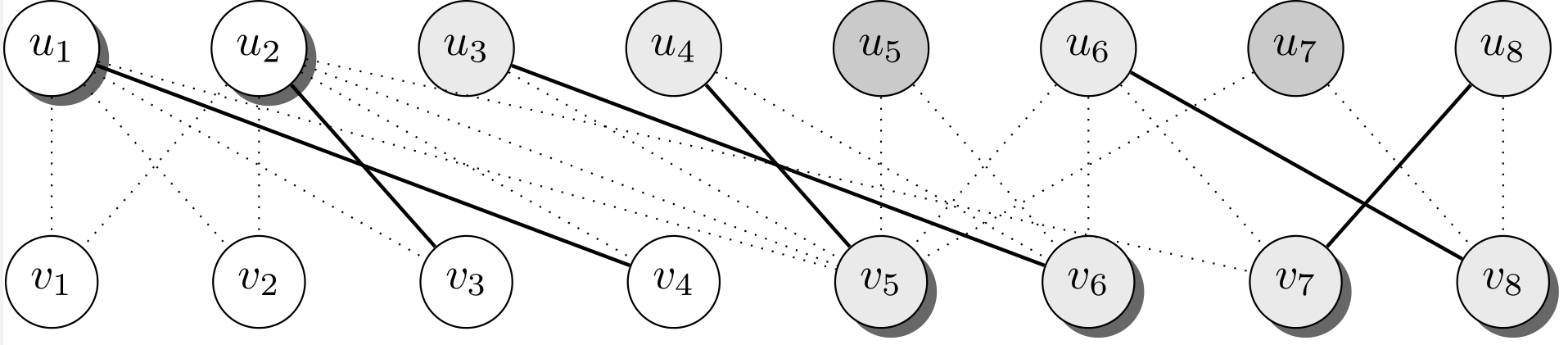
Now let S be $(U\setminus Z) \cup (V\cap Z)$. All edges of $M$ have either both endpoints in Z or none. Therefore we have $|S|=|M|$, which is the smallest cardinality a vertex cover can have (because it must cover already the edges of M). In the picture above, the vertices of S are indicated with a shadow.
But is it really a vertex cover? Yes, because there is no edge between $U \cap Z$ to $V\setminus Z$ as we observed earlier.
Here is an implementation of this algorithm.
Generalization for general graphs
Vertex Cover is an NP-hard problem for general (non bipartite) graphs. A 2-approximation can be computed in polynomial time, and assuming the unique game conjecture this is the best we can hope for.