Mirror maze
Given a grid with two openings and two sided mirrors in some grid cells, find an orientation for the mirrors at 45 or -45 degrees, such that a laser beam entering one opening would be reflected all the way to the second opening.
An \( O(n^2) \) algorithm
We use the following graph representation for this problem. Every mirror a generates up to 4 vertices, one for each direction up, left, down, right. If some mirror b is reachable from a in direction d then there is a vertex (a,d) and by symmetry a vertex (b,inv(d)) — where the inv function inverts the direction — and these vertices are connected by an edge. In addition vertices (a,d) and (a,e) are connected by an edge if d and e are adjacent directions. This construction is completed with a vertex for each of two openings. Each opening vertex is connected to the reachable mirror (if any). The opening vertices are connected together by an edge, or — variant of the graph model — connected each to an additional vertex. We distinguish two kind of edges: (i) horizontal or vertical ones and (ii) diagonal or anti-diagonal ones.
We claim that the graph has a perfect matching if and only if the mirror maze instance has a solution. The interpretation of a matching is the following. A vertical or horizontal edge in the matching means that the laser does not follow this trajectory. A diagonal or anti diagonal edge in the matching, say ((a,d),(a,e)), means that the laser reflects on the mirror a without however distinguishing the case that the laser enters a from direction d and leaves in direction e or the opposite case. Note that if there are two reflections happening on a mirror then these are not conflicting and there is a unique corresponding mirror position.
The algorithm consists of
- building the graph model,
- creating a near perfect matching, consisting of all horizontal and vertical edges. This corresponds to the complete absence of the laser beam.
- tries to build a perfect matching, by searching for a single alternating augmenting path,
This last step is hard to implement as it needs Edmond’s blossom algorithm.
Example
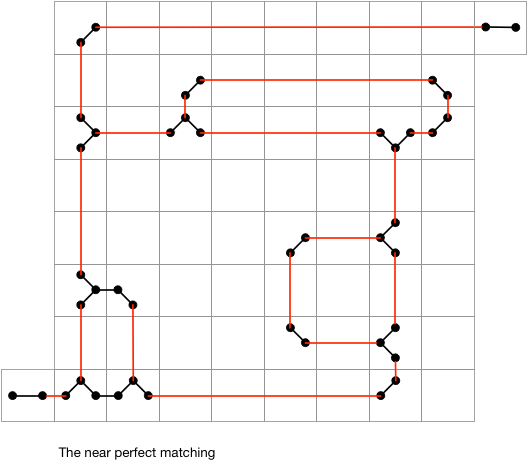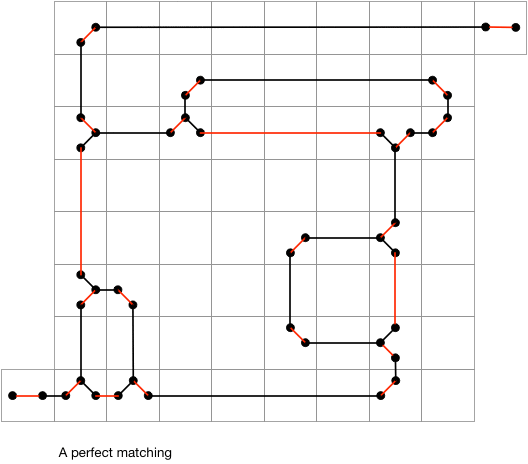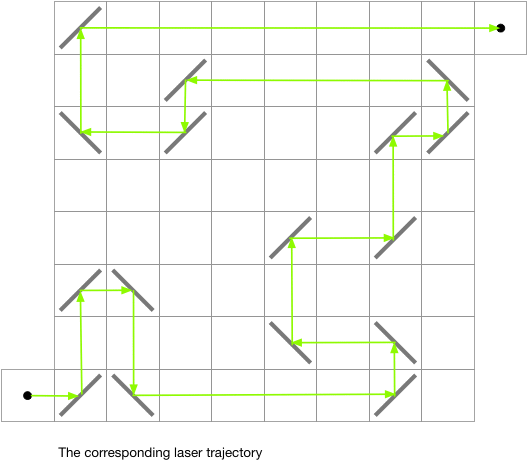
Note
The mirror maze problem can be solved with backtracking. Such a solution is of course not running in polynomial time in the worst case, but seems to pass all the tests and is quite easy to implement. But such a solution is cheating, wouldn’t you agree ?
References
Most available implementations of Edmond’s blossom algorithm are a bit long (who can blame?), but the following by David Eppstein is quite elegant:
