King's Wish
A K by K grid has to be tiled with L by W tiles which can be taken vertically or horizontally. Given K find L, W such that this tiling is possible and (max(L,W)-min(L,W), L+W) is lexicographically maximal subject to W < L < K. All numbers are positive integers.
(this document has been updated in December 2021)
A theorem about tilings
For every valid L, W pair we must have that L and W divide K. This is a theorem from the late 1960’s. At the end of this document is a link to 14 different proofs for this theorem, here is one. Given a fixed tiling of the grid, we construct a graph as follows. In fact it will be a multi-graph, as some edges might be present twice. The vertices consists of all points which are corners of individual tiles. For every tile, for each of its long side, there is an edge between the adjacent corners. This defines a graph with the following properties:
- the 4 corners of the grid have degree 1.
- all other points have degree 2 or 4.
Such a graph consists in a collection of paths and cycles. So if you start a walk from the lower left corner (with coordinates (0,0)), and make sure that you don’t walk over the same edge twice, then you must end in another corner of the grid. Such a corner has coordinates (0,K), (K,K) or (K,0). The coordinates of the intermediate points along the path all have coordinates which are multiplies of L. This proves that L divides K.
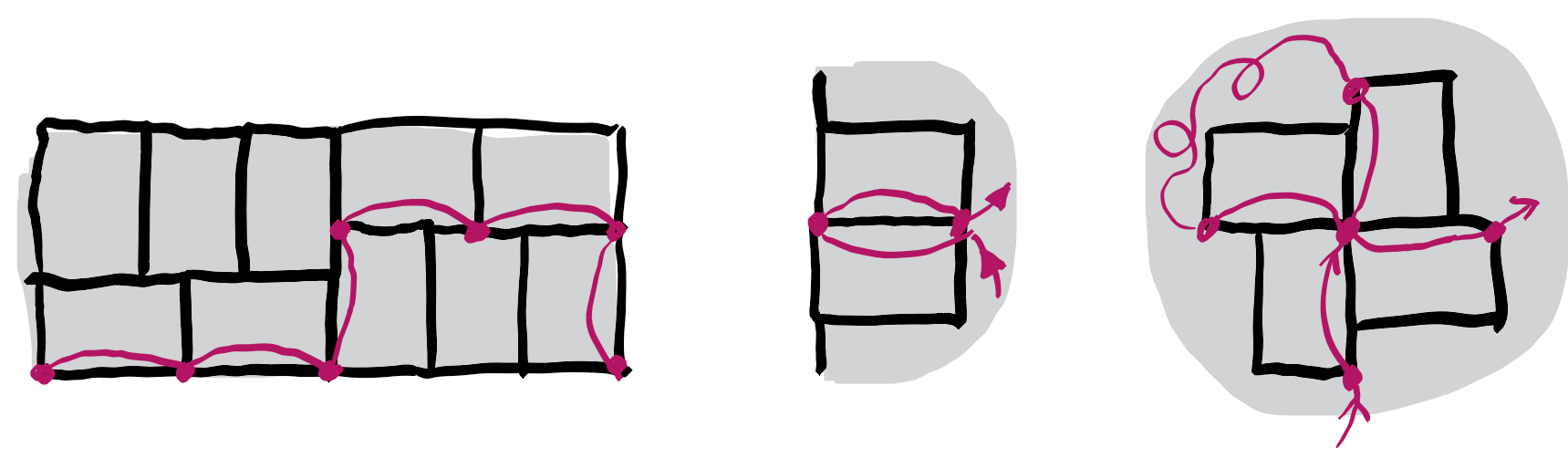
The same argument can be used to show that W divides K as well. The problem statement required that no smaller square can be tiled, which means that K is the least common multiple (lcm for short) of W and L.
Factorization of K
Suppose that K can be written as the product $p_1^{k_1}\cdots p_a^{k_a}$, for $a$ different primes, and positive integer exponents. Since both W and L divide K, they can be written as
\[W = p_1^{w_1}\cdots p_a^{w_a}\]and
\[L = p_1^{l_1}\cdots p_a^{l_a}.\]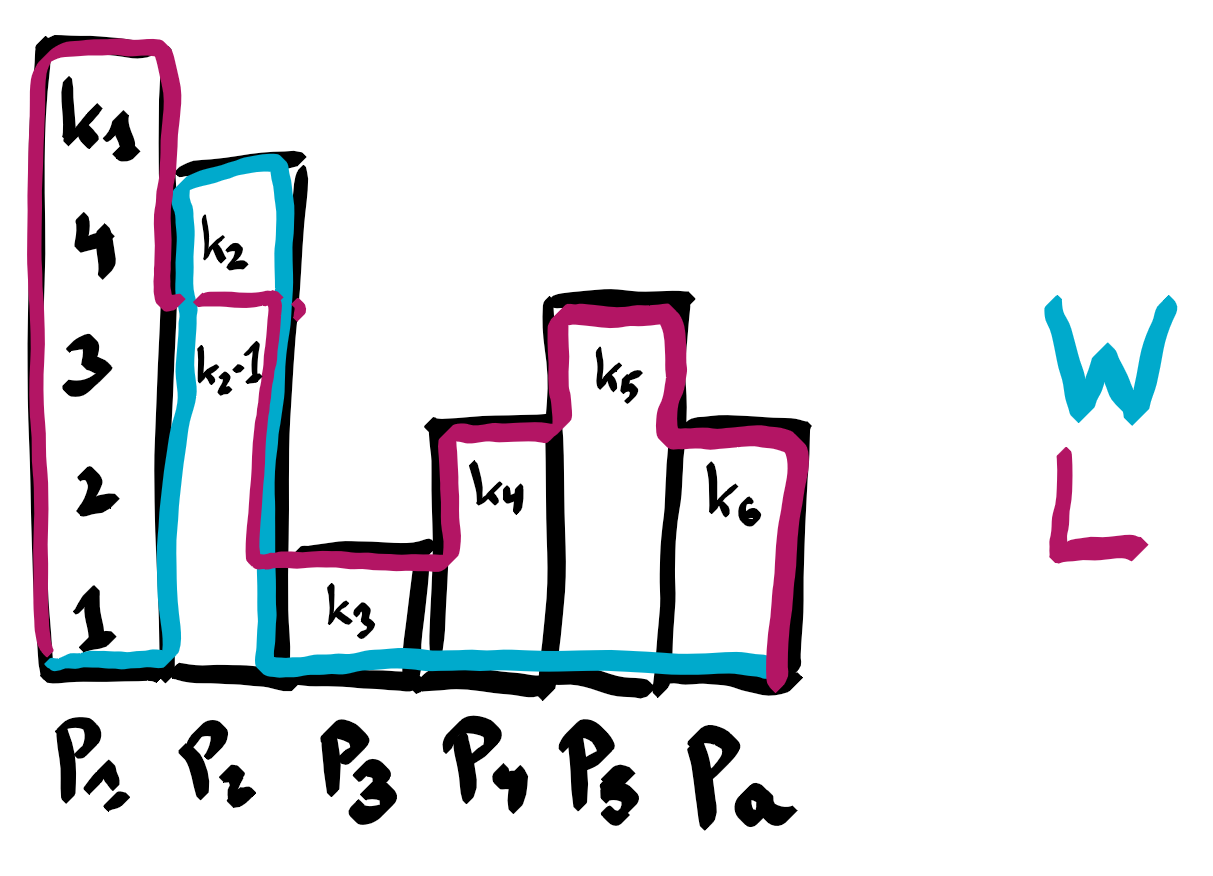
Since lcm(W,L)=K, we have $\max\{w_i,l_i\}=k_i$ for every $i=1,\ldots,a$. Since L < K, we know that for at least one index $i$, we have $l_i < k_i$, which implies $w_i = k_i$. Since the difference L - W must be largest possible, we can assume $l_i = k_i-1$. Now we claim that for an optimal pair (L,W) we have $W = p_i^{k_i}$ and $L=K/p_i$. Indeed if for some index $j\neq i$, $l_j < k_j$, then $w_j=k_j$ and exchanging $l_j$ with $w_j$, increases the difference L - W, by the assumption W < L. Also if for some index $j\neq i$, $l_j=k_j$, then setting $w_j=0$ does not increase W.
The algorithm
This means that we can solve the problem as follows.
- In a pre-processing step, generate all primes numbers up to a million, which is the square root of the upper bound on K.
- Decompose K into a product of prime factors $p_1^{k_1}\cdots p_a^{k_a}$.
- Return the pair $(L=K/p_i, W=p_i^{k_i})$ which maximizes L - W and in case of tie L + W.
In Python
The implementation below does not pass the timelimits, which seem to be too harsh for Python. Here we implemented the sieve of Eratosthenes.
import sys
def readint(): return int(sys.stdin.readline())
MAX = 1_000_001
is_prime = [True] * MAX
primes = []
for p in range(2, MAX):
if is_prime[p]:
primes.append(p)
for i in range(p * p, MAX, p):
is_prime[i] = False
def factorize(K):
L = []
for p in primes:
e = 0
while K % p == 0:
e += 1
K //= p
if e:
L.append((p, e))
if K > 1:
L.append((K, 1))
return L
def solve(K):
factors = factorize(K)
best = (0, 0, 0, 0)
for p, e in factors:
alt_W = p ** e
alt_L = K // p
alt = (alt_L - alt_W, alt_L + alt_W, alt_L, alt_W)
best = max(best, alt)
return best[2:]
testCases = readint()
for t in range(1, testCases + 1):
K = readint()
L, W = solve(K)
if L:
print(f"Case {t}: {L} {W}")
else:
print(f"Case {t}: Impossible")In C++
Here we implemented the sieve of Gries-Misra, just for a change. But the sieve of Eratosthenes is good enough for this problem.
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
typedef long long int64; // needed to store 10**12
const long MAX = 1000001L; // there are about 78000 primes less than 1E6
vector<int64> primes; // list of prime numbers less than MAX
int64 factor[MAX] = {0}; // for all x >= 2: factor[x] = smallest divisor of x
/** creates the list of all primes up to MAX
and fills table factor, such that factor[x] is smallest factor of x.
In particular factor[p]==p for all primes p.
*/
void gries_misra() {
for (int64 x=2; x < MAX; x++) {
if (factor[x] == 0) {
primes.push_back(x);
factor[x] = x;
}
for (int64 p: primes) {
if (p > factor[x] || p * x >= MAX)
break;
factor[p * x] = p; // p is the smallest factor of p * x
}
}
}
/** Returns list of all pairs <p,a> with the meaning that p**a divides k,
* for p prime and a maximal. These pairs might not be in order.
**/
vector<pair<int64, int>> factorize(int64 k) {
vector<pair<int64, int>> factors;
int64 w = 0;
// first we find divisors, by going through the list of primes
if (k >= MAX)
for (int64 p: primes) {
int expo = 0; // find out how many times p divides k
while (k % p == 0) {
expo++;
k /= p;
}
if (expo)
factors.push_back(make_pair(p, expo));
if (k < MAX) // switch to more comfortable factorization
break;
}
// if we run out of divisors from the list of primes, then the current k itself is prime
if (k >= MAX)
factors.push_back(make_pair(k, 1));
else // comfortable factorization using array factor
while (k > 1) {
int64 p = factor[k];
int expo = 0; // find out how many times p divides k
while (factor[k] == p) {
expo++;
k /= p;
}
factors.push_back(make_pair(p, expo));
}
return factors;
}
/** Find the best pair (L,W) with the described form
*/
pair<int64,int64> solve(int64 k) {
int64 best_ell = 0, best_w = 0;
vector<pair<int64, int>> fac = factorize(k);
for(pair<int64, int> p: fac) { // for all p**a in the factorization
int64 w = 1; // candidates: w=p**a and l=k/p
for (int i = p.second; i >= 1; i--)
w *= p.first;
int64 ell = k / p.first;
int64 diff = best_ell - best_w; // which candidate is the best?
int64 add = best_ell + best_w;
if (ell - w > diff || (ell - w == diff && ell + w > add)) {
best_ell = ell;
best_w = w;
}
}
if (best_ell > best_w) // is not the case if k the power of a single prime
return make_pair(best_ell, best_w);
else
return make_pair(0L, 0L);
}
int main() {
gries_misra();
int testCases;
cin >> testCases;
for (int t=1; t<=testCases; t++) {
int64 K;
cin >> K;
pair<int64,int64> lw = solve(K);
if (lw.first)
cout << "Case " << t << ": " << lw.first << " " << lw.second << endl;
else
cout << "Case " << t << ": Impossible" << endl;
}
return 0;
}References
A related theorem with 14 proofs