Making pairs adjacent at minimal cost
You are given an array $X$ with the promise that each of its values appears exactly twice. You want to transform $X$ such that at the end all pairs are adjacent in the array. An allowed operation consists in removing a value from $X$ and appending it at the end. The cost of a solution is the maximal value which was moved.
Simplification
The original problem description at Kattis involves two arrays, allowing to move values not only within an array but also between the arrays. We can reduce this variant to a single array problem, by concatenating the arrays into a single one. We just need to add two copies of a big enough value $M$ as a separator between the arrays. $M$ can be taken as the upper bound on the values, plus one. The example below is the sample input from the original problem description using $M=10$ as a separator.
Example
X = 2 1 8 2 8 10 10 9 9 4 1 4
2 8 2 8 10 10 9 9 4 1 4 1 # 1 moves to the end
8 2 8 10 10 9 9 4 1 4 1 2 # 2 moves to the end
8 8 10 10 9 9 4 1 4 1 2 2 # 2 moves to the end
8 8 10 10 9 9 4 4 1 2 2 1 # 1 moves to the end
8 8 10 10 9 9 4 4 2 2 1 1 # 1 moves to the end
this solution has cost 2
A threshold based solution
Consider a solution of cost $T$. The cost $T$ really means that we can move all values $x$ of value at most $T$. So $T$ plays the role of a threshold. The threshold is valid, if in the table restricted to all values greater than $T$, the values are pairwise adjacent. In the example above this would give 8 8 10 10 9 9 4 4 if we choose $T=2$.
This leads to a first solution with time complexity $O(N \log M)$. We have the promise that all values are strictly between 0 and M. Hence we can do a binary search on this interval, to find the smallest valid threshold. Deciding if a given threshold is valid can be done in linear time in N, by going through the table, keeping track of values above $T$, and checking if every other value equals the previous one. This is the solution described by the problem setters at the competition NWERC2016 (see slide 8), and is probably the simplest to come up with. So in a programming competition, this is the solution you want to go for. But since we are not in hurry, let’s see if we can find a solution with a time complexity independent of $M$.
A maximum range query based solution
Here is another important observation on this problem. Suppose that some value $y$ appears in the array at indices $i$ and $j$. Then if both copies of $y$ are not adjacent, i.e. the range $[i+1,j-1]$ is not empty, then some values have to move in order to make the copies adjacent. If $z$ is some value in $X$ in this range, then at least one of $y,z$ has to move. Therefore if $z$ is the maximum value in $X$ between the indices $i+1$ and $j-1$ (included), then the threshold is at least $\min\{y,z\}$. So if we store $X$ in a maximum-range-query data structure, then we can answer these range queries in time $O(\log N)$, and solve the problem in time $O(N\log N)$ by considering the lower bounds on the threshold generated by all value pairs $y$ in $X$. Let’s see if we can get rid of the logarithmic factor.
A solution with optimal time complexity
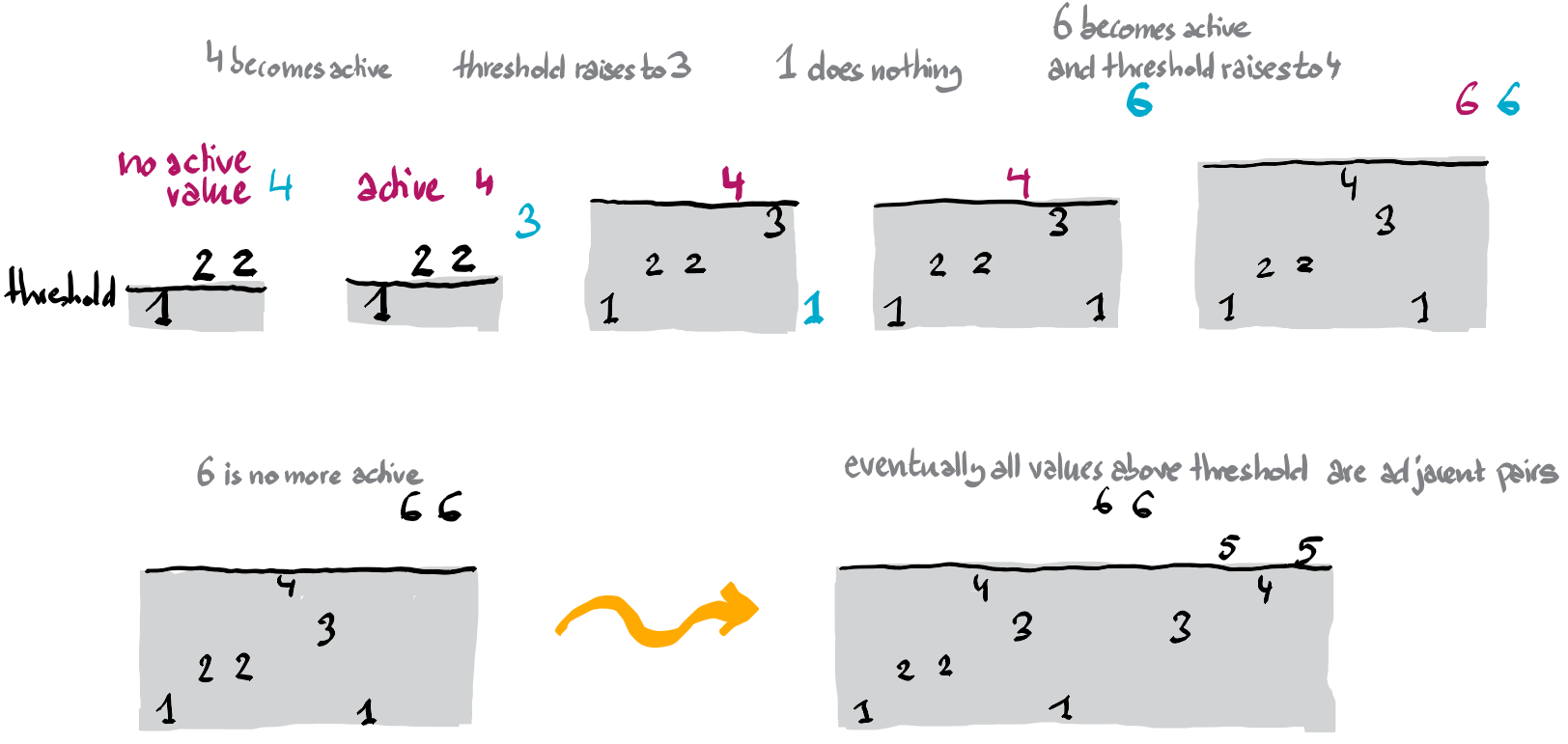
We want to find the smallest valid threshold $T$. The idea is to scan $X$ from left to right and to increase $T$ whenever we are forced to. At any moment we will have seen at most one value $A$ above the current threshold for which we haven’t seen the second copy yet. Such a value is said to be active. If there is no active value, we set $A$ to zero.
Suppose we already processed the first $i-1$ values of $X$, and are now processing value $x=X[i]$. Now it is only a matter of comparing $x$ with $T$ and $A$, see figure below.
- If $x$ is larger than the threshold $T$ and there is no active value ($A=0$), then $x$ becomes active.
- If $x$ is strictly between $T$ and $A$ (implying that there is an active value), then the threshold must be raised to $x$. Why? Because both copies of $A$ (the second is still to come) are separated by value $x$.
- If $x$ equals $A$, then we are happy, because we found the second copy of the active value. Now we set $A$ to zero, indicating that we don’t have any active value anymore.
- If $x$ is larger than both $T$ and $A$, and there is an active value, then we have to raise the threshold to $A$. Because both copies of $A$ (the second is still to come) are separated by $x$. At the same time $x$ becomes the active value.
- It remains the case is when $x$ does not exceed the threshold. But nothing is to be done in that case.
Finally when we are done processing the whole array, why is the resulting threshold valid? Well, notice that all values above the threshold came in pairs, and were active at some point. Life is beautiful, really!
Implementation in Python
import sys
def readstr(): return sys.stdin.readline().rstrip()
def readint(): return int(readstr())
def readints(): return list(map(int, readstr().split()))
n = readint()
M = 1_000_000_001 # separator between rows
row = readints() + [M, M] + readints() # make single row
threshold = 0
active = 0 # zero means no active value
for x in row:
if threshold < x and active == 0:
active = x
elif threshold < x < active:
threshold = x
elif x == active:
active = 0
elif threshold < active < x:
threshold = active
active = x
print(threshold)