November Rain
You are given $n$ non intersecting line segments in the 2 dimensional plane. The segments are not parallel to the x-axis, nor to the y-axis and segments do not intersect. These segments represent roofs, and it is raining. Water flows down along the roofs, and pours from the lower endpoint to the roof below if there is one. The task is to compute how much water each roof receives.
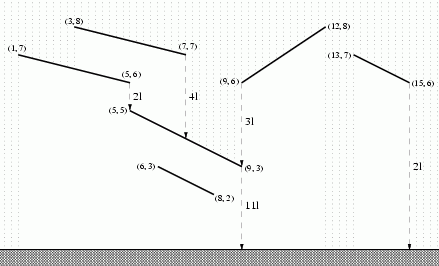
You are given the promize that above every point of the line, there are at most 25 line segments.
Topological sorting
One difficulty is to find out which roof pours on which roof. For this we compute a table, such that down[i] contains the index of a roof recieving the water from roof i.
Another difficulty is to find out how much direct rain each roof recieves. We store this quantity in a table rain.
Once we have this information, we can consider the directed graph, where every roof is a vertex and has at most one outgoing arc, as defined by the down table. We can then simply process the roofs in topological order, cumulating in an array water the water each roof recieves. Initially water[i]=rain[i]. And when processing roof i, we simply update water[down[i]] += water[i].
Sweepline algorithm
We would like to solve this problem with a sweepline algorithm. One approach would be to scan the roofs from top to bottom following the rain direction. But then we don’t exploit the structural property of at most 25 segments above each point. It is better to scan the segments from left to right. For every position x, we maintain a list of all segments above x, in a bottom-top order. Whenever a segment enters we can sequentially search the list to find the insertion point. Very simple, don’t even need to implement a binary search for such small lists. So when the lowest point of a roof enters or leaves the list, we can identify the roof below it and store this information in the down table. At the same time, when the the position x is moved delta units to the right, we can add delta to the variable rain[i], where i is the top of the list.
Complexity
The overall algorithm has complexity $O(n \log n)$, with a multiplicative constant of 25. This is ok, given n is 40.000.
