Skip to main content Link Search Menu Expand Document (external link)
    

Covering points with a strip

• geometry •
Related problems: [swerc:Blowing candles]

Given n points in the 2-dimensional plane find a strip with minimal width that covers all the points.

Convex hull

The key observation is that a narrowest strip touches at least 2 successive points a, b on the convex hull on one side of the strip and a point c on the convex hull on the opposite side.

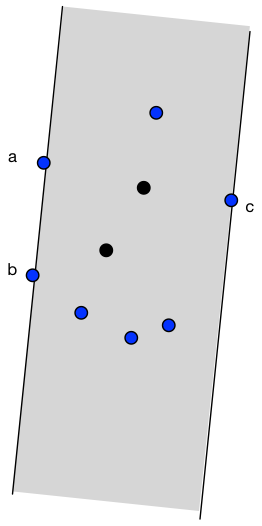
Strip

This leads to the following algorithm.

  • Compute the convex hull of the points, and restrict to these points.
  • Loop over every pair of successive points a, b on the hull, and maintain a point c that is furthest to the line a-b.
  • Return the smallest observed point-to-line distance.

The first step takes time $O(n\log n)$, while the second step takes time $O(n)$.

Implementation

In computational geometry problems you want to avoid the use of trigonometric functions, and do all the computations if possible using only integer additions and multiplications. Just two computational geometry tools are necessary to solve the above problem. One is to determine the orientation of a point c with respect to the directed line defined by two points a and b.

def left_turn(a, b, c):
    return (a[0] - c[0]) * (b[1] - c[1]) - (a[1] - c[1]) * (b[0] - c[0]) > 0

And the second needed tool is the computation of the squared distance between a point p0 and a line defined by points p1 and p2. Squaring the distance is a trick that enables to stay within integer computations and even saves some computational time.

def dist2(p0, p1, p2):
    x0, y0 = p0
    x1, y1 = p1
    x2, y2 = p2
    num = ((y2 - y1)*x0 - (x2 - x1)*y0 + x2 * y1 - y2 * x1) ** 2
    denom = (y2 - y1)**2 + (x2 - x1)**2
    return float(num) / denom

Convex hull

For the convex hull you can use Grahams algorithm or Andrew. Personally I prefer the last one, but they are not much different.

def andrew(S):
    S.sort()
    top = []
    bot = []
    for p in S:
        while len(top) >= 2 and not left_turn(p, top[-1], top[-2]):
            top.pop()
        top.append(p)
        while len(bot) >= 2 and not left_turn(bot[-2], bot[-1], p):
            bot.pop()
        bot.append(p)
    return bot[:-1] + top[:0:-1]

Further applications

This algorithm is called Rotating calipers and can be used to solve various related problems, such as for example:

  • finding the furthest pair of points of a given set,
  • compute the diameter of a convex polygon,
  • compute the distance between two polygons,
  • compute the smallest rectangular bounding box for a set of rectangles.

Comments

Related posts