Dessiner sans lever le crayon !
Introduction
Vous connaissez à peu près tous (si vous n’êtes pas trop jeunes ?) ce jeu où il fallait dessiner une maison sans repasser sur un même trait.
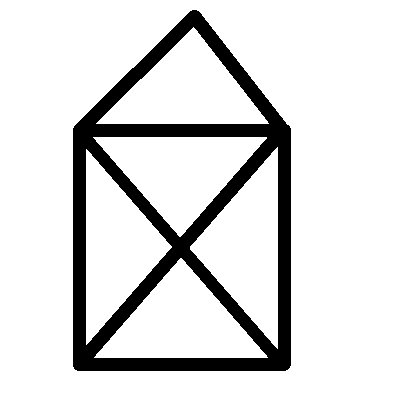
Quel traumatisme, en y repensant. Certaines personnes (i.e. Wikipédia) appellent aussi ce dessin une enveloppe ouverte
Bon, en général, soit vous deviniez l’astuce, soit on vous la montrait une fois, et vous la reteniez suffisamment longtemps pour pouvoir proposer l’énigme à vos petits camarades à votre tour. Vous posez votre crayon au niveau du point en bas à gauche, puis vous suivez les flèches rouges dans l’ordre croissant des indices :
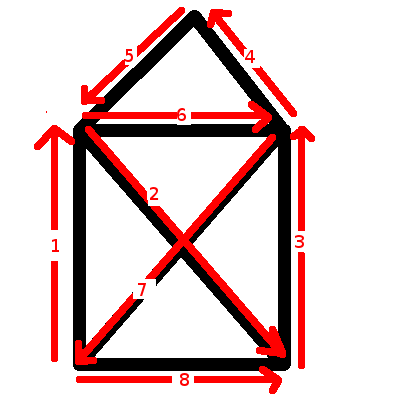
Imaginez-vous (de retour) à l’école primaire. L’une de vos congénères, une certaine Jeanne-Léonie d’Euler, s’approche de vous, et vous demande si vous connaissez l’énigme de la maison décrite ci-dessus, et vous propose une variante. Confiant.e, vous acquiesçez, et vous vous apprêtez à vous vous la ramen… à démontrer l’étendue de votre savoir modestement acquis. Or cette petite rabouine, comme vous allez vite comprendre, vous présente le dessin suivant :
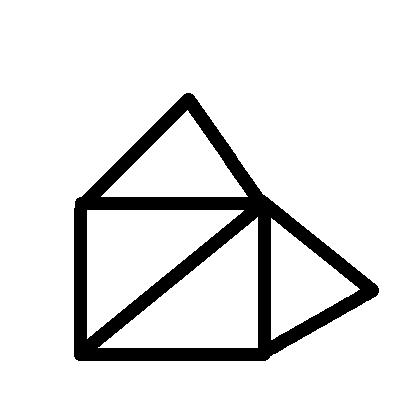
Je vous arrête : ce dessin signe la fin de votre réputation auprès des énigmes à l’école. Il existe une solution, mais elle est vicieuse (oui, parfaitement !), dans le sens où vous devez replier un coin de la feuille sur lequel passer votre crayon pour pouvoir revenir à un point du dessin inaccessible autrement pour pouvoir tracer le dernier trait du dessin par exemple.
En résumé : il existe des dessins que l’on peut (respectivement, ne peut pas) tracer sans lever le crayon sur une même surface (excluant donc la solution vicieuse, je maintiens, décrite ci-dessus). Ne serait-il pas fort sympathique de pouvoir caractériser les dessins traçables, c’est-à-dire, décrire précisément les propriétés de ces dessins qui permettent d’affirmer qu’ils sont traçables sans lever le crayon ? Pour la science, bien sûr, mais aussi pour sauter dans une machine à remonter le temps, et aider votre vous-même du passé à montrer votre supériorité sur la damoiselle Euler, pardon, à partager votre savoir et à ne pas tuer votre grand-père.
Le problème du chemin eulérien
Ce problème peut se ramener à un problème sur un graphe (lisez l’article sur l’algorithme de Dijkstra pour une définition formelle des graphes). On convertit un dessin en graphe non orienté en définissant chaque bris de ligne comme un noeud, et chaque ligne comme une arête. Le but est alors de trouver un moyen de parcourir tous les arêtes du graphe (tracer le dessin), en ne passant qu’une seule fois sur chaque arête (ce qui correspond à la contrainte de ne pas repasser sur un même trait), et en allant seulement d’une arête à une arête qui lui est adjacente (c’est-à-dire qui partage un même noeud, ce qui correspond à la contrainte de ne pas lever le crayon). Le chemin d’arêtes résultant est appelé un chemin eulérien (merci Euler, Léonard celui-là).
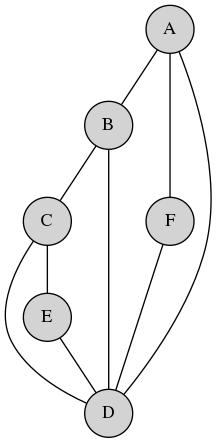
(Le dessin incriminé converti en graphe)
Le problème peut être étendu aux graphes orientés, multi-arêtes (c’est-à-dire avec possiblement plusieurs arêtes entre deux noeuds donnés), … mais par souci de concision, on ne va s’attarder que sur les graphes non orientés, simples.
Résolution
On peut former une petite intuition sur les dessins, donc les graphes, qui seront traçables. Premièrement, on veut que toutes les arêtes soient accessibles en partant de n’importe quel noeud non isolé (donc relié à au moins une arête), autrement dit, que le graphe soit connexe. Deuxièmement, à l’exception éventuelle du premier et/ou du dernier noeud du chemin, on souhaiterait qu’à chaque fois que l’on arrive à un noeud, on puisse “en sortir”, i.e. qu’il reste une arête non empruntée que l’on puisse utiliser. On peut donc imaginer que la caractérisation sur les graphes portera d’une certaine façon sur la parité des arêtes des noeuds (intermédiaires du chemin).
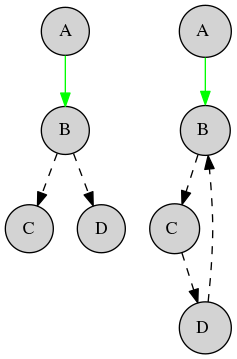
Si le chemin déjà tracé est colorié en vert, on voit que le dessin de gauche ne peut être tracé sans lever le crayon, alors que le dessin de droite l’est (en suivant l’orientation des flèches en pointillés).
Introduisons le théorème d’Euler-Hierholzer :
Un graphe (connexe) est eulérien si et seulement si chacun de ses sommets est relié à un nombre pair d’arêtes.
La preuve de ce théorème par Hierholzer est disponible ici, et, quoiqu’instructive, j’estime qu’elle sort un peu du cadre de cet article. L’idée principale à retenir est l’intuition ci-dessus, à savoir que l’on arrivera toujours à “sortir” d’un noeud dans un graphe eulérien jusqu’à épuisement de toutes les arêtes disponibles pour chaque noeud. Voici un exemple simple de graphe eulérien :
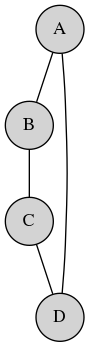
Mais là, vous re-regardez l’exemple de la première maison, et vous vous exclamez à juste titre : “Mais on avait deux noeuds avec un nombre impair d’arêtes (3), et pourtant nous avons réussi à tracer cette maison !”. Et effectivement, le fait qu’un graphe soit eulérien n’est pas nécessaire pour pouvoir le tracer sans lever le crayon (mais est suffisant !).
Essayez donc de tracer la première maison sans partir ni du noeud 7, ni du noeud 2/8. Lors du tracé d’un chemin, vous resterez “coincé” dans l’un de ces deux noeuds. Cela confirme l’intuition que les premier et dernier noeuds n’ont pas à être soumis à la contrainte décrite dans le théorème ci-dessus. Un graphe connexe qui vérifie la contrainte dans le théorème sur ses noeuds exceptés exactement deux d’entre eux est appelé semi-eulérien, et ceci constituera la caractérisation finale des dessins traçables sans lever le crayon.
En effet, si on note A et B les deux noeuds avec un nombre impair d’arêtes, en ajoutant l’arête A-B au graphe, on obtient un graphe eulérien (par définition), et on sait que ces graphes sont traçables sans lever le crayon. On note C un chemin possible (donc, la succession d’arêtes à emprunter) pour tracer le graphe sans lever le crayon. On peut commencer ce chemin à partir de n’importe quelle arête, commençons donc par l’arête A-B. Alors le chemin C, privé de l’arête A-B, est un chemin eulérien pour le graphe de départ (utilise toutes les arêtes, une seule fois, successivement). Donc ce dernier est traçable sans lever le crayon.
Implémentation en Python
Il reste à tester de façon algorithmique le degré (c’est-à-dire, le nombre d’arêtes reliées à) des noeuds du graphe en entrée. Si on choisit la représentation en matrice d’adjacence d’un graphe non orienté simple, on peut calculer le degré d’un noeud en sommant les coefficients de la colonne d’indice associé à ce noeud. Puis on compte le nombre de noeuds de degré impair.
# M est la matrice d'adjacence (liste de colonnes de la matrice)
def est_tracable(M):
n = len(M)
# Sommer les coefficients de chaque colonne de M
# degres[i] donne le degré du coefficient d'indice i
degres = [sum(M[i]) for i in range(n)]
nb_impair = 0
for i in range(n):
# Si degres[i] modulo 2 (le reste de degres[i] par 2) est égal à 1
# i.e. si degres[i] est impair
if (degres[i]%2 == 1):
nb_impair += 1
# On retourne Vrai si le graphe est eulérien ou semi-eulérien
return(nb_impair == 0 or nb_impair == 2)
On teste pour l’exemple de la première maison :
M1 = [
[0, 1, 1, 1, 1],
[1, 0, 1, 1, 0],
[1, 1, 0, 1, 0],
[1, 1, 1, 0, 1],
[1, 0, 0, 1, 0]
]
print(est_tracable(M1))
> True
On teste pour l’exemple donné par Jeanne-Léonie :
M2 = [
[0, 1, 0, 1, 0, 1],
[1, 0, 1, 1, 0, 0],
[0, 1, 0, 1, 1, 0],
[1, 1, 1, 0, 1, 1],
[0, 0, 1, 1, 0, 0],
[1, 0, 0, 1, 0, 0]
]
print(est_tracable(M2))
> False
Pour aller plus loin
On a un problème similaire pour trouver un chemin qui, cette fois, ne passe qu’une seule et unique fois par chaque noeud du graphe. Un graphe qui admet un tel chemin est appelé hamiltonien. La résolution du problème du chemin hamiltonien est largement plus dure, en termes de temps de calcul, que celle du graphe eulérien.