Comment planifier une todo-list ?
Introduction
Bonjour, on est en septembre et c’est la rentrée ! Ah, ce florilège de paperasse, de pluie, de salles toutes sombres où l’on reste quatre heures, et ce doux fumet de légère déprime (à moins que ce soit l’odeur du renfermé) qui s’en exhale. Idéal avec le café du matin.
Désormais, vous devez (ré)apprendre à avoir des choses à faire, et à les accomplir. Mais comme vous le savez fort bien, certains de ces devoirs ne peuvent s’accomplir qu’à partir du moment où d’autres tâches sont achevées, nécessitant de les effectuer dans un certain ordre si vous voulez vous assurer de terminer toute votre todo-list. A ce moment-là, vous ne savez littéralement pas par où commencer. Le but de cet article sera donc de pouvoir planifier les tâches à accomplir pour pouvoir compléter votre liste.
Par exemple, pour pouvoir suivre vos cours avec une relative sérénité, à moins de déjà posséder un logement sur place, vous devez vous trouver une chambre universitaire avant le début des cours. Cette chambre ne vous sera fournie que si vous présentez un certificat de scolarité, pour pouvoir prétendre au logement étudiant. Vous n’accèderez à ce certificat qu’en complétant un dossier à remettre à la scolarité, qui n’est ouverte qu’à partir du moment où les cours commençent.
(The story, all names, characters, and incidents portrayed in this production are fictitious.)
Formalisation
C’est bon, vous suivez ? Pour simplifier la représentation de votre épopée, dessinons un graphe orienté où les noeuds seront les tâches à accomplir/les évènements permettant d’accéder à une tâche, et où l’arc de la tâche (ou évènement) A à la tâche (ou évènement) B signifie “A doit être accomplie (respectivement s’être produite) pour que l’on puisse commencer B (resp. que B puisse se produire)”, ou plus généralement, “B dépend de A”. Naturellement, on a envie par ce moyen de décrire une succession des tâches à accomplir qui nous permette de ne pas nous retrouver dans une impasse où l’on ne peut finir une tâche car on n’a pas tous les pré-requis qui lui sont nécessaires.
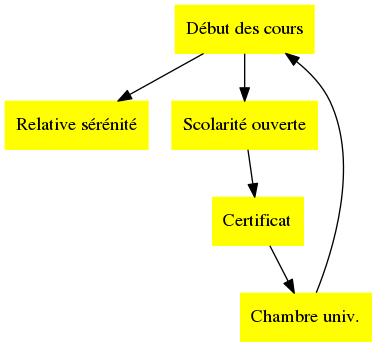
La relation décrite par les arcs s’appelle une relation de dépendance. Le graphe décrivant l’ensemble de ces relations est un graphe de dépendances. Une succession de tâches à effectuer dans l’ordre et qui permet d’obtenir tous les pré-requis avant chaque tâche s’appelle un ordre d’évaluation. On constate qu’un tel ordre n’existe pas forcément : en l’occurrence, on voit bien grâce au précédent graphe de dépendances qu’il n’est pas possible d’assister aux cours, car intuitivement, on observe que l’on ne peut pas obtenir de chambre universitaire avant le début des cours (soupir).
Premières idées
La détection d’ordres d’évaluation impossibles se fait, comme dans l’exemple ci-dessus, par la reconnaissance de cycles de dépendances, ici, le cycle “Début des cours” -> “Scolarité ouverte” -> “Certificat” -> “Chambre universitaire” -> “Début des cours”. On voit donc que le graphe de dépendances est très pratique, car il permet de faire ressortir facilement les impasses dans l’exécution de tâches. “Facilement”, dans le sens où l’on peut concevoir un algorithme qui puisse les identifier sans notre supervision. Si c’était relativement évident dans l’exemple précédent, il est beaucoup plus dur de détecter manuellement ces problèmes dans des graphes beaucoup plus larges, comme, par exemple, lorsque l’on veut effectuer une suite d’instructions : si le programme est { a = 4; c = a + b; retourner c }, où a, b, c sont trois variables entières, et que la valeur de b n’a pas été initialisée, on aura un problème pour retourner la valeur de c !
>>> a = 3
>>> c = a + b # Python râle
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
NameError: name 'b' is not defined
Pour ceux et celles plus expertes en programmation, c’est aussi grâce aux graphes de dépendances que vous allez passer deux heures à installer une bibliothèque parce que vous n’avez pas les bonnes versions de SuperPackageTM numéro i, où i est compris entre 1 et 100.
Prenons maintenant un autre exemple. Préparons-nous un chocolat chaud (à défaut d’avoir un logement). Pour cela, il faut faire bouillir de l’eau, puis verser l’eau dans un mug, sortir un sachet de chocolat en poudre (bonjour tristesse), et enfin, mélanger la poudre et l’eau.
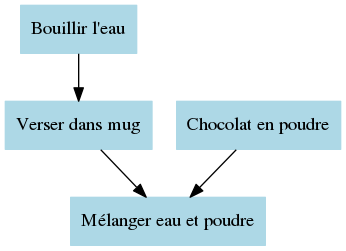
Ce graphe-là ne présente pas de cycle : on appelle ce type de graphe acyclique orienté (Directed Acyclic Graph, en anglais). Intuitivement, on va pouvoir trouver un ordre d’évaluation sur ces graphes. On va décrire mathématiquement l’ordre d’évaluation comme une fonction qui prend en argument un noeud du graphe et va retourner l’indice de la tâche dans l’ordre d’évaluation : par exemple, un ordre d’évaluation (pas forcément unique, comme le montre cet exemple !) pour le graphe ci-dessus peut être la fonction f telle que :
- f(“Bouillir l’eau”) = 1
- f(“Verser dans mug”) = 2
- f(“Chocolat en poudre”) = 3
- f(“Mélanger eau et poudre”) = 4
i.e. on effectue “Bouillir l’eau” en premier, puis “Verser dans mug”, etc. Une succession de tâches, dépendant l’une de l’autre deux à deux, est nommée une chaîne de dépendances (par exemple, “Bouillir l’eau” -> “Verser dans mug” -> “Mélanger eau et poudre”).
Mais comment inférer automatiquement des ordres d’évaluation ?
Résolution (Algorithme de Kahn, 1962)
Premièrement, on sait qu’il faut voir si le graphe possède des cycles (par exemple, en faisant un parcours du graphe, et en regardant si, lors du parcours, on tombe sur un noeud que l’on a déjà visité), puisqu’on sait que l’on ne trouvera pas de tels ordres sur ce graphe. Deuxièmement, une première idée est de, par la suite, commencer par regarder les noeuds sans arcs entrants (donc, les noeuds qui n’ont aucune dépendance), puisque ce sont les tâches que l’on pourra effectuer en premier. Ensuite, on pourra voir à quelles tâches on peut accéder (i.e. que l’on pourra effectuer) en ayant terminé les choses associées aux noeuds sans dépendances. Puis, récursivement, on pourra regarder quelles tâches seront nouvellement accessibles, jusqu’à ce que l’on ait visité tous les noeuds du graphe.
Essayons d’appliquer cette méthode au graphe ci-dessus, avant de passer à l’implémentation.
- Choisissons un noeud sans dépendances (arbitrairement) : “Bouillir l’eau”, par exemple. On associe le numéro 1 à ce noeud.
- Regardons les tâches nouvellement accessibles. Seulement la tâche “Verser dans mug” est accessible. On associe alors le numéro 2 à ce noeud.
- Regardons les tâches nouvellement accessibles. Aucune tâche n’est accessible, et il reste des noeuds non visités. On va donc choisir un nouveau noeud sans dépendances. Ce noeud existe forcément, car le graphe a un nombre de noeuds non visités fini, non nul, et n’a pas de cycle : il existe du coup au moins une chaîne finie (de longueur finie) de noeuds non visités (éventuellement réduite à un seul noeud), et on peut alors considérer le premier noeud de cette chaîne, qui n’aura pas de dépendances. Ici, on peut choisir “Chocolat en poudre”. On associe le numéro 3 à ce noeud.
- Regardons les tâches nouvellement accessibles. La tâche “Mélanger eau et poudre” est maintenant accessible. Associons-lui le numéro 4.
- Regardons les tâches nouvellement accessibles. Aucune tâche n’est accessible, et tous les noeuds sont visités : on retourne l’ordre d’évaluation que l’on a obtenu.
On peut observer aussi du coup que la détection des graphes cycliques peut aussi s’effectuer à l’intérieur de l’algorithme (et non plus en faisant un parcours de graphe au préalable, ce qui peut être sympathique pour réduire le temps de calcul) : on peut regarder si on ne trouve pas de noeud sans dépendances/noeuds accessibles alors qu’il reste des noeuds non visités (condition 1) ou si on n’a pas déjà attribué un numéro d’évaluation à l’une des tâches nouvellement accessibles (condition 2). Si c’est le cas, on est alors tombé sur un cycle, et on retourne une erreur.
Sinon, on retourne l’ensemble des numéros de noeuds, qui constitue ce que l’on appelle un tri topologique, noté f, qui satisfait la condition suivante : pour tous noeuds a et b du graphe, si f(a) < f(b), alors (b, a) (“a dépend de b”) n’est pas un arc du graphe.
Implémentation en Python
Ecrivons la procédure associée en Python. On utilise l’implémentation en listes d’adjacence du graphe.
On remarque en fait que les noeuds sans dépendances sont des tâches accessibles (hé oui !) dès le début de l’algorithme. Forts de cette observation, pour faciliter l’implémentation, on ne va donc garder en mémoire qu’une seule liste de noeuds (au lieu d’une pour les noeuds sans dépendances, et une pour les tâches nouvellement accessibles).
Pour faciliter la compréhension, on garde une liste de noeuds accessibles, et un tableau ordre qui dénote les noeuds non visités et visités (on pourrait ne conserver que le tableau ordre qui dénoterait les noeuds non visités non accessibles, accessibles, et visités).
# L est la liste des listes d'adjacence du graphe de dépendances
def kahn(L):
# n nombre de noeuds
n = len(L)
# numéro d'évaluation courant à attribuer
i = 0
# ordre d'évaluation à compléter
# si ordre[noeud] == 0 alors on a accès au noeud mais on ne l'a pas traité
# si ordre[noeud] > 0 alors on a traité le noeud
ordre = [0]*n
# on initialise la liste des noeuds accessibles
# par les noeuds sans dépendances non visités
# i.e. les noeuds qui n'apparaissent dans aucune
# liste d'adjacence
# On agrège les listes d'adjacence
avec_dep = [dep for liste in L for dep in liste]
accessibles = []
for noeud in range(n):
if (not(noeud in avec_dep)):
accessibles.append(noeud)
# S'il n'existe pas de noeuds sans dépendances
# alors on a trouvé un cycle (condition 1 de cycle)
if (len(accessibles) == 0):
return []
# tant que l'on n'a pas visité tous les noeuds
while (len(accessibles) > 0):
# Sinon, retirer un noeud dans la liste des noeuds
# sans dépendances non visités
noeud = accessibles.pop()
# Si ordre[noeud] > 0 (noeud déjà visité)
# alors on a trouvé un cycle (condition 2 de cycle)
if (ordre[noeud] > 0):
return []
# Sinon, attribuons le numéro i à ce noeud
i += 1
ordre[noeud] = i
# Regardons les tâches nouvellement accessibles
# depuis noeud
# i.e. où tous les noeuds dont elles dépendent
# ont été traités
for no in L[noeud]:
# Listons les dépendances restant non résolues de no
dep_non_resolues = []
for nn in range(n):
if (no in L[nn]):
if (ordre[nn] == 0):
dep_non_resolues.append(nn)
# et supprimons les dépendances résolues
else:
L[nn].remove(no)
# no est accessible si et seulement si
if (len(dep_non_resolues) == 0):
accessibles.append(no)
# Si on ne trouve pas de noeud accessibles
# et qu'il y a encore des noeuds non visités
# on a alors trouvé un cycle (condition 1 de cycle)
if (len(accessibles) == 0 and i < n):
return []
# et on itère !
return(ordre)
On teste les exemples précédents :
# "Début des cours" = noeud 0, "Scolarité ouverte" = noeud 1,
# "Certificat" = noeud 2, "Chambre univ." = noeud 3,
# "Relative sérénité" = noeud 4
exemple1 = [
# Noeuds auxquels on accède directement par le noeud 0
# i.e. les noeuds qui dépendent du noeud 1
[1, 4],
# Noeuds auxquels on accède directement par le noeud 1
[2],
[3],
[0],
[]
]
print(kahn(exemple1))
# Indices 0 1 2 3 4
> []
# "Bouillir l'eau" = noeud 0, "Verser dans mug" = noeud 1,
# "Chocolat en poudre" = noeud 2, "Mélanger eau et poudre" = noeud 3
exemple2 = [
# Noeuds auxquels on accède directement par le noeud 0
[1],
# Noeuds auxquels on accède directement par le noeud 1
[3],
[3],
[]
]
print(kahn(exemple2))
# Indices 0 1 2 3
> [2, 3, 1, 4]
Pour aller plus loin
On peut aussi énumérer en modifiant cette méthode tous les ordres d’évaluation possibles sur le graphe. Les seules variations entre les ordres d’évaluation d’un même graphe de dépendances vont, d’après l’algorithme de Kahn, porter sur la sélection arbitraire de noeuds, que ce soit au niveau de la prochaine tâche accessible à traiter, ou des noeuds sans dépendances (qui ne sont au final que des tâches nouvellement accessibles particulières). De manière générale, on appelle niveau les noeuds qui sont ou seront accessibles en même temps (autrement dit, ils ont les mêmes dépendances ou la même absence de dépendances). Pour cela, on énumère tous les ordres possibles sur chacun des niveaux, et, pour chaque ordre, on lance la procédure décrite ci-dessus, en ne choisissant plus les noeuds arbitrairement, mais selon l’ordre que l’on s’est fixé préalablement (si un noeud est placé devant un autre dans un ordre, on sélectionnera ce noeud en premier lors de l’étape de choix de noeuds accessibles).
Une autre méthode a été introduite par Tarjan en 1976, et utilise un parcours de graphe (tiens !) en profondeur. En effet, si on attribue un indice (décroissant, en commençant par le nombre n égal au nombre de noeuds dans le graphe) à chaque noeud que l’on a visité (en commençant par visiter les fils d’un noeud, i.e. les tâches qui dépendent de ce noeud, plutôt que ses frères, qui sont les tâches qui sont accessibles en même temps que le noeud considéré), on obtient également un ordre d’évaluation.