Trouver un plus court chemin grâce à Google Ma... Dijkstra
Contexte
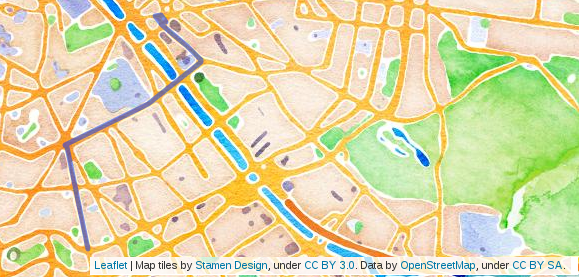
Le problème de la recherche d’un plus court chemin entre deux points est le suivant :
Etant donnés :
- Un graphe (autrement dit, une carte);
- Un point de départ A;
- Un point d’arrivée B;
On veut trouver :
- un chemin entre A et B, passant par des routes de la carte, qui minimise une certaine quantité : par exemple, dans l’image du dessus, le chemin représenté est un chemin qui minimise la distance entre ses deux extrémités.
Notamment, on peut vouloir minimiser le temps de trajet, le coût, … (et on peut noter qu’il peut exister plusieurs chemins qui ont la même valeur de temps ou de coût : donc il peut exister plusieurs plus courts chemins).
Il est facile de concevoir qu’un tel problème a de nombreuses applications. Ce qui est peut-être moins évident, c’est que vous n’aurez pas à sortir la carte Michelin et la calculatrice : l’ordinateur peut faire le boulot à votre place assez rapidement. Même sur de très grandes cartes. Et cela, c’est génial -et ça, l’équipe technique derrière Google Maps l’a bien compris.
Notations sur les graphes
Qu’est-ce qu’un graphe ? Je vous ai fait avaler cela en vous disant que c’était proche d’une carte, mais ce n’est guère satisfaisant. Plus prosaïquement, un graphe est un sac dans lequel on a :
- Un ensemble de noeuds V (comme “vertices”), aussi appelés sommets (les cercles numérotés dans l’image);
Le plus souvent, on associe un entier à chaque noeud.
- Un ensemble d’arêtes E (comme “edges”), qui sont les segments qui lient deux noeuds.
Un graphe est non orienté si les arêtes entre deux noeuds peuvent être parcourues dans les deux sens : autrement dit, si j’ai un chemin d’un noeud a à un noeud b, alors j’ai aussi un chemin de b vers a. On en conclut que dans un graphe orienté, si j’ai une arête entre a et b, je ne peux a priori aller de a vers b mais pas de b vers a.
Voici un exemple de graphe orienté :
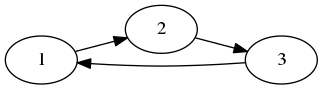
On représente souvent dans ce cas-là une arête allant de a vers b avec la notation (a, b) avec a et b deux entiers correspondant à deux noeuds du graphe (en particulier, a peut être égal à b…).
Par exemple, le graphe ci-dessus s’écrit :
V = {1, 2, 3}
E = {_, (1, 2), _, _, _, (2, 3), (3, 1), _, _}
(Vous verrez plus tard la raison d’une telle mise en page.)
Voici un exemple de graphe non orienté :
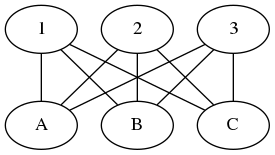
On représente souvent dans ce cas-là une arête avec la notation {a, b} avec a et b deux entiers correspondant à deux noeuds du graphe (en particulier, a peut être égal à b…).
Par exemple, le graphe ci-dessus s’écrit :
V = {1, 2, 3, 4, 5, 6}
E = {{1, 2}, {1, 3}, {1, 4}, {1, 5}, {1, 6},
{2, 1}, {2, 3}, {2, 4}, {2, 5}, {2, 6},
{3, 1}, {3, 2}, {3, 4}, {3, 5}, {3, 6},
{4, 1}, {4, 2}, {4, 3}, {4, 5}, {4, 6},
{5, 1}, {5, 2}, {5, 3}, {5, 4}, {5, 6},
{6, 1}, {6, 2}, {6, 3}, {6, 4}, {6, 5}}
que l’on peut simplifier en, sachant que le graphe est non orienté :
E = {_, {1, 2}, {1, 3}, {1, 4}, {1, 5}, {1, 6},
_, _, {2, 3}, {2, 4}, {2, 5}, {2, 6},
_, _, _, {3, 4}, {3, 5}, {3, 6},
_, _, _, _, {4, 5}, {4, 6},
_, _, _, _, _, {5, 6},}
(Ce n’était pas le graphe le plus court à décrire, mais il a le mérite de bien tester les définitions).
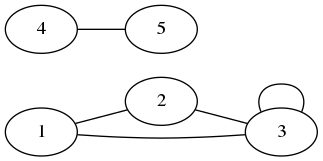
Exercice : décrire les graphes ci-dessous.
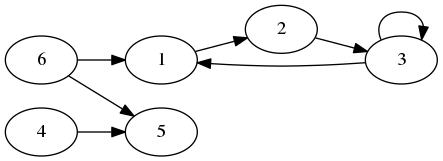
Représentation en mémoire d’un graphe
Comment implémenter un graphe, autrement dit, définir un graphe dans un langage appréhendable par un ordinateur ?
Réponse : Il y a plusieurs façons, par exemple (applicable aux graphes non orientés et orientés) :
- Représentation en listes d’adjacence : exactement de la même façon que ci-dessus.
Un graphe est constitué de deux tableaux, l’un contenant les entiers associés aux noeuds, et l’autre (les listes d’adjacence) qui contient dans la case i les arêtes sortant du noeud associé à l’entier i. Par exemple dans le deuxième exemple de l’exercice ci-dessus, les arêtes sortant du noeud 2 sont {2, 1} et {2, 3}. Dans le premier exemple, l’unique arête sortant du noeud 2 est (2, 3).
On se rend compte que, quitte à renommer les noeuds avec des étiquettes comprises entre 1 et n, le nombre total de noeuds du graphe, on peut laisser tomber le premier tableau qui ne fait qu’énumérer les nombres de 1 à n. A noter que comme, en général, en programmation, les tableaux sont indexés à partir de 0, il est préférable d’étiqueter les noeuds entre 0 et n-1.
- Représentation en matrice d’adjacence :
Pour la même raison que précédemment, on laisse tomber le tableau énumérant les étiquettes des noeuds.
On représente les arêtes entre les noeuds par une matrice, c’est-à-dire un tableau de nombres. Voici une matrice, avec pour chaque case, la position correspondant à cette case :
(0, 0), (0, 1), (0, 2) (1, 0), (1, 1), (1, 2)
La position est donc notée (n, m), où n est le numéro de ligne (en partant de 0), et m le numéro de colonne (en partant de 0).
Pour une matrice d’adjacence, le coefficient en position (n, m) vaut 1 s’il existe une arête allant du noeud n au noeud m; sinon, il vaut 0.
Par exemple, pour ce graphe :

La matrice d’adjacence correspondante est :
0, 1, 0
0, 0, 1
1, 0, 0
Pour ce graphe :

La matrice d’adjacence correspondante est :
0, 1, 1, 1, 1, 1
1, 0, 1, 1, 1, 1
1, 1, 0, 1, 1, 1
1, 1, 1, 0, 1, 1
1, 1, 1, 1, 0, 1
1, 1, 1, 1, 1, 0
que l’on peut simplifier en, sachant que le graphe est non orienté (donc qu’on a les mêmes coefficients de chaque côté de la diagonale) :
0, 1, 1, 1, 1, 1
0, 0, 1, 1, 1, 1
0, 0, 0, 1, 1, 1
0, 0, 0, 0, 1, 1
0, 0, 0, 0, 0, 1
0, 0, 0, 0, 0, 0
(D’où l’intérêt de la mise en page précédente !)
Il existe d’autres méthodes. Mais on ne s’y attardera pas plus.
Un exemple concret
Vous êtes un touriste à Paris qui n’a malheureusement pas le temps de flâner dans les rues de la capitale. Vous préparez donc soigneusement l’itinéraire du lendemain, qui doit dans un premier temps vous amener de votre hôtel à la Tour Eiffel, le plus vite possible.
On suppose que vous avez déjà à votre disposition une carte de la ville avec un certain nombre de points, reliés entre eux par des chemins étiquetés par le temps en minutes nécessaire pour passer d’un point à l’autre (de manière générale, on suppose ici que les coûts des chemins sont positifs). Parmi ces points figurent la Dame de fer (française) E et votre hôtel H.
Evidemment, vous pourriez trouver tous les chemins partant de H et allant à E sur la carte, calculer le coût total (dans notre cas, additionner les temps) et comparer à la fin de cet éreintant travail les différents coûts et choisir le chemin qui a le coût le plus faible. Vous pourriez même réduire le nombre de chemins à regarder en essayant de minimiser le nombre de noeuds et en évitant les boucles. Mais même pour l’ordinateur, cette stratégie est coûteuse et peut ne pas donner le bon résultat.
Méthode
L’astuce est de réfléchir sur le choix d’un chemin localement, c’est-à-dire, si l’on est sur un point P de la carte, regarder les autres points auxquels P est directement relié par un chemin, et choisir celui noté A qui est le plus proche de P, dont l’étiquette du chemin A-P est la plus petite parmi celles des autres points reliés à P. L’idée peut paraître surprenante. Si l’opéra Garnier est l’endroit le plus proche de mon hôtel, aller à Opéra alors que je veux visiter la Tour Eiffel ne semble pas avoir grand intérêt. Mais si j’accède à Opéra à une ligne de métro qui me transporte en 20 minutes au parc du Trocadéro, alors qu’avancer dans la direction de la Tour Eiffel me forcera à aller me perdre dans les petites rues de la ville, ce choix peut avoir du sens. C’est d’ailleurs une stratégie typiquement gloutonne (mais si, on en a déjà parlé dans l’article sur le rendu de monnaie), puisqu’elle consiste à faire un choix jugé optimal sans connaître les possibilités qui se présenteront plus tard.
Algorithme de Dijkstra (1959)
L’algorithme de Dijkstra, qui est un des algorithmes les plus connus, et celui qui parmi eux présente le plus petit coût en temps -une fois programmé avec la bonne structure de données, c’est-à-dire avec la description des objets utilisés dans l’algorithme, par exemple les graphes, la moins coûteuse possible- exploite précisément l’idée que pour trouver le plus court chemin entre deux points, il faut à chaque fois chercher le plus court chemin depuis le point de départ H en allongeant la distance entre H et le point d’arrivée considéré à une étape de l’algorithme.
Plus exactement, on construit un ensemble de points S de la carte, au début uniquement constitué du point de départ, que l’on va grossir à chaque étape de la façon suivante : on considère les points directement reliés à l’un des éléments de S, et plus particulièrement les coûts des chemins qui les relient à un élément de S. On parcourt l’ensemble de ces coûts, et on recherche le plus petit d’entre eux. Puis on regarde à quel chemin correspond ce coût (il peut y en avoir plusieurs : on en choisit un). On ajoute à S l’extrémité de ce chemin qui n’y appartenait pas déjà, et on met à jour la distance qui sépare ce point de ses voisins par rapport au point de départ. Puis on itère jusqu’à ce que S contienne tous les points de la carte.
Sans se préoccuper de l’implémentation qui peut être un peu technique (jouant tout de même un rôle capital dans le temps mis par l’algorithme pour trouver la solution, au niveau de la structure de données), ni de la représentation de la carte que vous avez en votre possession, l’algorithme général se présente donc ainsi :
Créer un ensemble S ne contenant que le point de départ
Créer un ensemble A des points accessibles en une étape depuis les points de S,
n appartenant pas à S
Créer un tableau D contenant les distances de chaque point de la carte depuis le
point de départ
(que l on initialise à l infini de partout sauf pour la case correspondant
au point de S, et pour les cases correspondant à des points dans A, valant
le nombre sur l arête entre le point dans A et le point dans S)
Tant que S ne contient pas tous les points de la carte
1) Chercher un point P dans A avec un coût minimal depuis un point de S, et le retirer de A
2) Pour chaque point B accessible en une étape depuis P faire
a) D[B] = minimum entre D[B] et D[P] + c (où c est l étiquette du chemin P-B)
b) Ajouter B à A
3) Ajouter P à S
Retourner D[point de départ, point d arrivée]Cet algorithme retourne donc le coût minimal entre le point de départ et le point d’arrivée. Et si nous voulions en plus récupérer un chemin qui vérifie ce coût à la fin de l’algorithme ?
Créer un ensemble S ne contenant que le point de départ
Créer un ensemble A des points accessibles en une étape depuis les points de S,
n appartenant pas à S
Créer un tableau D contenant les distances de chaque point de la carte depuis
le point de départ (que l on initialise à l infini de partout,
sauf pour la case correspondant au point de départ, qui vaut 0,
et pour les cases correspondant à des points dans A, valant le nombre sur l arête
entre le point dans A et le point dans S)
Créer un tableau Pred dont les cases sont non définies
(sauf pour la case correspondant à S, valant le point dans S)
Initialiser pere égal au point de départ
Tant que S ne contient pas tous les points de la carte
1) Chercher un point P dans A avec un coût minimal depuis un point de S,
et le retirer de A
2) Pour chaque point B accessible en une étape depuis P faire
a) D[B] = minimum entre D[B] et D[P] + c (où c est l étiquette du chemin P-B)
b) Ajouter B à A
3) Pred[P] = pere
4) pere = P
5) Ajouter P à S
Initialiser arrivee égal au point d arrivée
Créer une liste L ne contenant que le point d arrivée
Tant que arrivee est différent du point de départ
1) arrivee = Pred[arrivee]
2) Ajouter arrivee à L
Retourner LLa terminaison est donnée exactement par ce que nous avons indiqué plus haut : la construction de S s’arrête quand tous les points de la carte appartiennent à S. En particulier, si n est le nombre de points de la carte et nS le nombre d’éléments de S, la quantité n-nS décroît strictement à chaque fois (et est entière évidemment).
Exemples
Vous n’avez rien compris ? C’est parfaitement normal. Et c’est à cela que servent les dessins (et les exemples) !
Prenons un plan de Paris simplifié (et probablement faux). Soient les points H (hôtel), E (Tour Eiffel), O (Opéra), C (Châtelet), M (musée Guimet), auxquels on associe respectivement les entiers 1, 2, 3, 4 et 5. Les entiers près des arêtes donnent le coût de transport entre deux noeuds, dans un monde idéal où les trajets en métro ont la plupart du temps un coût nul sur le temps de trajet et la santé mentale des usagers.

On voit clairement que le trajet le moins coûteux ici est le trajet H->C->O->M->E. Testons si l’algorithme précédent retourne ce résultat.
On initialise (revoir les définitions) S = {H}, A = {C}.
point 1 2 3 4 5
D = [0, +inf, +inf, 0, +inf]
point 1 2 3 4 5
pred = [H, ND, ND, ND, ND]
pere = H
On note e(a, b) la valeur de l’entier sur le chemin entre a et b.
** Comme S = {H} ne vaut pas {H, C, O, M, E} : **
On récupère l'unique point dans A, qui est C
On retire C de A
Le seul point accessible en une étape depuis C est O
On met à jour D (O est associé à 3, C est associé à 4) :
D[3] = +inf
D[4] + e(O, C) = 0 + 0 = 0
On affecte donc la valeur 0 à la case D[3]
On ajoute O à A
On affecte donc la valeur H à la case Pred[4]
On affecte C à la variable *pere*
On ajoute C à S
** Comme S = {H, C} ne vaut pas {H, C, O, M, E} : **
On récupère l'unique point dans A, qui est O
On retire O de A
Les points accessibles en une étape depuis O sont M et E
On met à jour D :
D[2] = +inf
D[3] + e(O, E) = 0 + 1 = 1
On affecte donc la valeur 1 à la case D[2]
On ajoute E à A
D[5] = +inf
D[3] + e(O, M) = 0 + 0 = 0
On affecte donc la valeur 0 à la case D[5]
On ajoute M à A
On affecte donc la valeur C à la case Pred[3]
On affecte O à la variable *pere*
On ajoute O à S
** Comme S = {H, C, O} ne vaut pas {H, C, O, M, E} : **
Comme e(O, E) > e(O, M), on récupère le point M dans A
On retire M de A
Les points accessibles en une étape depuis M sont E et O
On met à jour D :
D[2] = 1
D[5] + e(M, E) = 0 + 0 = 0
On affecte donc la valeur 0 à la case D[2]
On ajoute E à A
D[3] = 0
D[5] + e(O, M) = 0 + 0 = 0
On ne change donc pas la valeur de D[3]
On ajoute O à A
On affecte donc la valeur O à la case Pred[5]
On affecte M à la variable *pere*
On ajoute M à S
** Comme S = {H, C, O, M} ne vaut pas {H, C, O, M, E} : **
On récupère l'unique point dans A, E
On retire E de A
Les points accessibles en une étape depuis E sont M et O
On met à jour D :
D[5] = 0
D[2] + e(M, E) = 0 + 0 = 0
On ne change donc pas la valeur de D[5]
On ajoute M à A
D[3] = 0
D[2] + e(O, E) = 0 + 1 = 1
On ne change donc pas la valeur de D[3]
On ajoute O à A
On affecte donc la valeur M à la case Pred[2]
On affecte E à la variable *pere*
On ajoute E à S
** Comme S = {H, C, O, M, E}, on s’arrête dans la boucle Tant que. **
Récupérons alors un chemin correspondant au coût minimal :
On initialise arrivee = E, et L = [E].
** Comme arrivee = E ne vaut pas H : **
On affecte donc la valeur Pred[2] = M à arrivee
On affecte donc la valeur [E, M] à L
** Comme arrivee = M ne vaut pas H : **
On affecte donc la valeur Pred[5] = O à arrivee
On affecte donc la valeur [E, M, O] à L
** Comme arrivee = O ne vaut pas H : **
On affecte donc la valeur Pred[3] = C à arrivee
On affecte donc la valeur [E, M, O, C] à L
** Comme arrivee = C ne vaut pas H : **
On affecte donc la valeur Pred[4] = H à arrivee
On affecte donc la valeur [E, M, O, C, H] à L
En remettant la liste à l’endroit, on obtient H->C->O->M->E. Magique, non ? (si la magie de l’algorithme ne vous touche pas, tant pis…)
Pour aller plus loin
La preuve de correction de cet algorithme consiste à démontrer un ou plusieurs invariants (c’est-à-dire des propriétés qui sont vérifiées à chaque étape de l’algorithme) un peu pénibles qui se basent sur la théorie des graphes et des arborescences, qui formalisent l’idée que l’on a récupéré à chaque étape de la construction de S les points à distance minimale du point de départ. Une autre idée de preuve qui marche (si rigoureusement écrite, ce qui n’est pas forcément évident…) est de considérer le chemin obtenu par l’algorithme, et un autre chemin entre H et E, et de montrer que ce dernier a un coût au moins égal à celui trouvé par l’algorithme. C’est une démarche classique pour démontrer la correction d’un algorithme glouton.
Détail important, les chemins doivent bien avoir des coûts positifs. Sinon, l’algorithme ne marche pas. En effet, il trouvera peut-être un chemin de l’hôtel vers la Tour Eiffel qui prendra pour être parcouru un temps strictement négatif. Outre les désagréments existentiels qui en résulteraient, le problème est surtout que le coût pour le parcourir diminuerait à chaque fois que vous l’emprunteriez. Donc l’algorithme vous dirait (sans vouloir faire de finalisme) que le plus court chemin entre votre hôtel et la Tour Eiffel serait une boucle que vous devriez parcourir pour toujours. Oui, c’est pire que ce que vous imaginiez.
Pour vraiment aller plus loin, l’algorithme de Dijkstra calcule en réalité une arborescence avec pour racine le point de départ. Késako ? En gros, une carte avec des chemins à sens unique, reliant tous les points sans faire de boucle, tel qu’il existe un unique point à partir duquel on peut accéder à tous les autres. Du mal à voir ? Dessinez un arbre (pas trop beau) avec uniquement des flèches, orientées du tronc vers les feuilles. Maintenant retournez votre feuille de papier. Tada ! On peut accéder depuis la racine de votre arbre (qui est normalement en haut de la feuille maintenant) à toutes les feuilles en suivant le sens des flèches.
Enfin, une démonstration intéressante de l’algorithme sur le graphe de Paris peut être vue ici (mais non, ce n’est pas une publicité déguisée).