Divide the land
Divide a trapezoid into two halfs of same area.
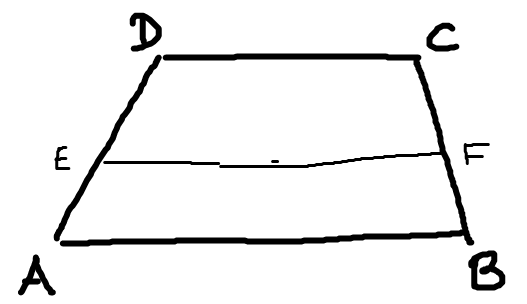
Input
A Trapezoid A-B-C-D
But only the edge lengths AB, BC, CD, DA are given.
Output
Points E,F such that EF is parallel to AB (and hence CD), and divides the trapezoid into two halfs of same area.
Solution
We aim for a value 0≤x≤1, such that when x=0, E=A, F=B and for x=1, E=D, F=C. More precisely E is a point on the segment AD at a position defined by x, and similarly is F on the segment BC.
Then EF = (1-x)AB + xDC.
The condition that both areas are the same gives:
((1-x)AB + xDC + AB)x h/2 = ((1-x)AB + xDC)(1-x) h/2
where h is the height of the trapezoid. We obtain
2(DC - AB) x^2 + 4AB - AB - DC = 0
and solve it for x.
double x = (-4*AB + Math.sqrt(16*AB*AB + 8*(CD - AB)*(CD + AB)))/(4*(CD - AB));
System.out.println("Land #"+land+": "+AD*x + " "+ BC*x);