Utiliser Paint pour les sudokus
Introduction
Vous vous souvenez du magnifique cliffhanger de l’article sur l’outil “Seau” de Paint ? (Bien évidemment. Sinon, vous êtes tout invités à le relire). On y avait découvert (un) algorithme de parcours des noeuds dans un graphe, et on l’avait utilisé pour implémenter l’outil “Seau” : en cliquant sur un pixel avec une certaine couleur, on colorie ce pixel, et tous ses pixels voisins de la même couleur initiale. En résumé :
- On convertit la grille de pixels de l’image en graphe: chaque noeud est un pixel, chaque noeud voisin (i.e., relié par une arête au noeud que l’on considère) est un pixel adjacent (qui partage un côté, ou parfois un coin, selon la définition de voisinage qui est choisie). Chaque noeud possède une propriété “couleur”, qui est la couleur actuelle du noeud.
- On commence par colorier le pixel que l’on a sélectionné avec l’outil : on remplace sa propriété “couleur” par la couleur que l’on a sélectionnée.
- On énumère tous les voisins de ce pixel dans le graphe de l’étape 1. Pour chacun d’entre eux, s’il est de la couleur à remplacer, alors on le colorie (étape 2), et on énumère ses voisins (étape 3) pour itérer la procédure. Sinon, on ne le modifie pas.
(Tout un article pour décrire cela, hé oui. Mais au moins, il y avait des illustrations de petits coeurs)
Et à la fin, j’avais écrit que l’on pouvait utiliser cet algorithme pour résoudre des sudokus. C’est donc parti !
Problème
Le sudoku est un jeu de puzzle où l’on doit compléter par des chiffres de 1 à 9 les cases vides d’une grille de 9 cases par 9, selon les trois règles suivantes :
- Chaque ligne contient une unique occurrence des chiffres 1 à 9.
- Chaque colonne contient une unique occurrence des chiffres 1 à 9.
- Chaque sous-grille de 3 cases par 3 contient une unique occurrence des chiffres 1 à 9.
Par exemple, la grille de sudoku incomplète suivante :
| Cases | A | B | C | D | E | F | G | H | I |
|---|---|---|---|---|---|---|---|---|---|
| a | 8 | 4 | 9 | 3 | 7 | 1 | |||
| b | 6 | 3 | 5 | 8 | 7 | 2 | 4 | ||
| c | 7 | 1 | 9 | 2 | 4 | 5 | |||
| d | 8 | 7 | 9 | 1 | 3 | 6 | |||
| e | 1 | 7 | 3 | 6 | 9 | ||||
| f | 3 | 6 | 4 | 8 | 2 | 1 | |||
| g | 6 | 5 | 4 | 7 | 3 | 8 | |||
| h | 4 | 7 | 3 | 2 | 1 | 9 | 5 | ||
| i | 9 | 5 | 1 | 8 | 4 | 2 |
peut être complétée en une grille complète et correcte de la façon suivante :
| Cases | A | B | C | D | E | F | G | H | I |
|---|---|---|---|---|---|---|---|---|---|
| a | 8 | [2] | 4 | 9 | [5] | 3 | [6] | 7 | 1 |
| b | 6 | 3 | 5 | 8 | [1] | 7 | [9] | 2 | 4 |
| c | 7 | 1 | 9 | [6] | 2 | 4 | [8] | 5 | [3] |
| d | [5] | 8 | 7 | [2] | 9 | 1 | 3 | [4] | 6 |
| e | 1 | [4] | [2] | 7 | 3 | 6 | [5] | [8] | 9 |
| f | 3 | [9] | 6 | 4 | 8 | [5] | 2 | 1 | [7] |
| g | [2] | 6 | [1] | 5 | 4 | [9] | 7 | 3 | 8 |
| h | 4 | 7 | [8] | 3 | [6] | 2 | 1 | 9 | 5 |
| i | 9 | 5 | [3] | 1 | [7] | 8 | 4 | [6] | 2 |
Les chiffres en gras permettent de faire ressortir les sous-grilles de 3 cases par 3 dont je parlais plus tôt.
Utiliser Paint ?
Sachant que l’on sait que l’on va utiliser la même méthode que l’outil “Seau”, comment fait-on pour ramener un problème de sudoku à un problème de coloriage de pixels ? Vous l’aurez deviné : on va convertir la grille de sudoku en graphe. Pour convertir ce problème en graphe, on doit donc déterminer :
- Quels seront les noeuds de ce graphe ?
- Quels seront les (éventuelles) propriétés des noeuds ? Quelles informations veut-on retenir à propos de ces noeuds ?
- Quelle définition de voisinage devra-t-on utiliser ?
Laissez-vous le temps de la réflexion avant de poursuivre. En particulier, prenez une feuille de papier, et écrivez une idée de réponse à ces deux questions. En particulier, repensez à ce qui a été fait pour l’outil Seau. Ce ne sera probablement pas l’exacte même formalisation qui sera utilisée, mais vous serez dans la bonne direction.
Faites-le.
Formalisation du problème
J’espère que vous avez noirci cette feuille de papier.
- Les noeuds seront les cases de la grille. Donc, en tout, le graphe aura 9 x 9 = 81 noeuds.
- On veut retenir la valeur de chaque noeud, autrement dit, la valeur de chaque case.
- Deux noeuds seront voisins si et seulement si (en utilisant les règles du sudoku) :
(a) Ils sont situés sur la même ligne.
(b) Ils sont dans la même colonne.
(c) Ils sont dans la même sous-grille 3 x 3.
Mais il manque une règle : celle de l’unique occurrence sur les lignes, colonnes et sous-grilles. Et c’est là où va intervenir la partie coloriage dans la résolution du problème : on attribue une couleur par valeur possible de case (autrement dit, 9). Le but sera alors de colorier le graphe de telle sorte à ce que, pour toute paire de noeuds voisins, ces deux noeuds aient des couleurs distinctes.
Par exemple, considérons une grille incomplète de sudoku 4 x 4 (pour plus de lisibilité…). En particulier, les sous-grilles seront de taille 2, et les lignes et les colonnes seront de longueur 2. On complétera la grille par les valeurs 1 (bleu), 2 (rouge), 3 (vert) ou 4 (orange) :
| Cases | A | B | C | D |
|---|---|---|---|---|
| a | 3 | 4 | ||
| b | 4 | 2 | 1 | |
| c | 3 | |||
| d | 1 | 3 | 4 | 2 |
(Je ne vous ferai pas l’insulte de vous donner la solution).
Le graphe correspondant est le suivant :
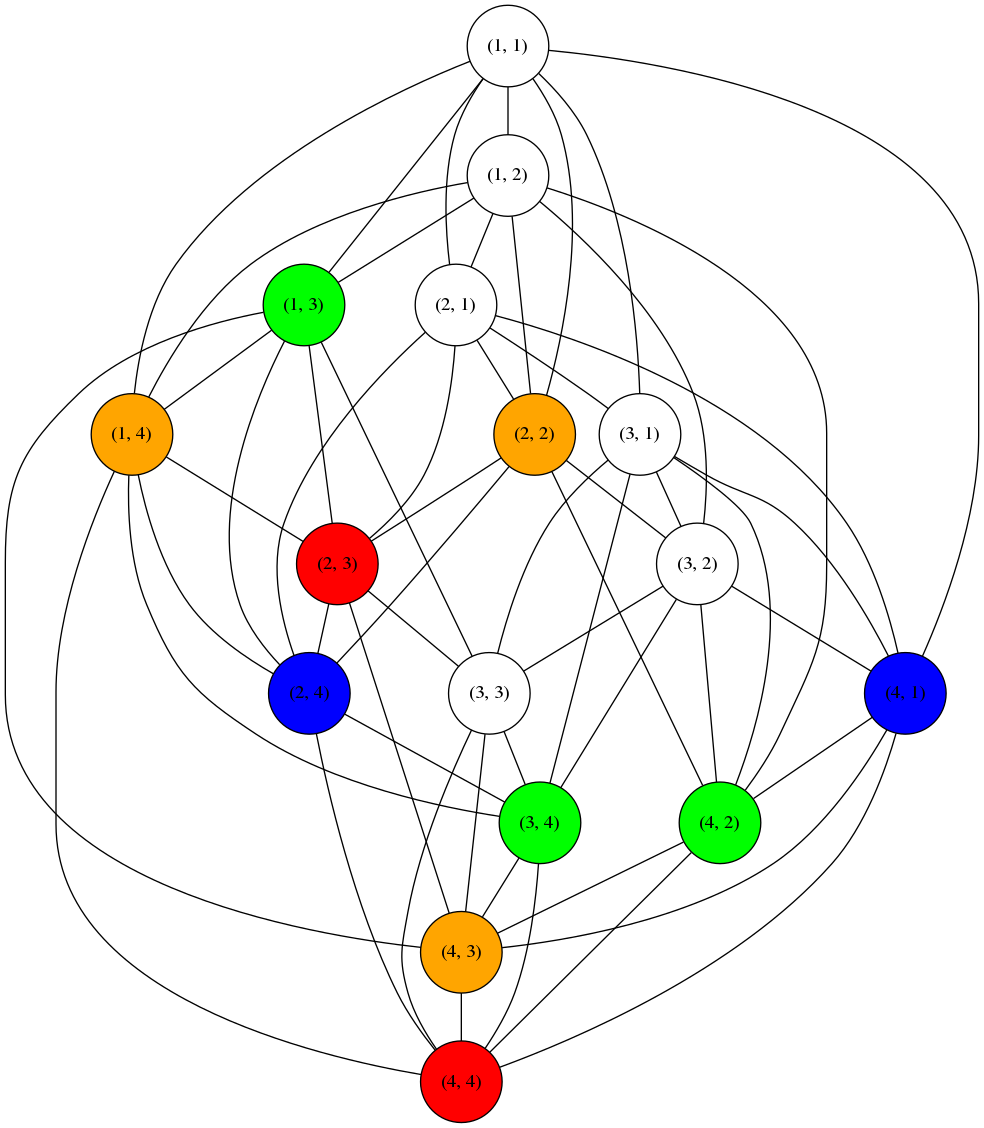
Maintenant que l’on a le graphe, comment procéder pour résoudre le problème de coloriage associé ?
Résolution du problème de coloriage
En quoi l’algorithme utilisé pour l’outil Seau va-t-il nous être utile ? En fait, les noeuds déjà coloriés nous donnent un ensemble de contraintes pour le choix de la couleur de leurs voisins. Essentiellement, l’algorithme consiste à rassembler toutes ces contraintes, à les propager aux voisins des noeuds déjà coloriés (comme la couleur pour l’outil Seau), et, à partir de ce moment-là, chercher les couleurs restantes qui peuvent être utilisées. A chaque nouveau noeud colorié, on réitère le processus de propagation de contraintes aux voisins, jusqu’à ce que tous les noeuds sont coloriés (et on trouve une solution), ou qu’un noeud ne puisse être colorié (car toutes les couleurs sont interdites pour ce noeud). Dans ce cas, on effectue un backtracking (voir cet article), et on revient à l’étape précédente, marque la couleur que l’on avait choisie à cette étape comme “interdite”, et on poursuit l’algorithme.
On associe donc à chaque noeud une propriété “couleurs interdites”, qui nous donne la liste des couleurs des voisins du noeud considéré.
A chaque étape de l’algorithme :
- Pour tout noeud déjà colorié, pour chacun de ses voisins, on ajoute la couleur de ce noeud à la propriété “couleurs interdites” des voisins.
- Si un noeud ne peut être colorié (car la propriété “couleurs interdites” contient toutes les couleurs disponibles), alors retourner “BACKTRACKING”/une exception/etc. (ce qui nous poussera à “backtracker”).
- Sinon, on cherche un noeud avec un nombre maximal de couleurs interdites, et on choisit une couleur qui ne fait pas partie de cette liste, et on le colorie avec cette couleur. On revient à l’étape 1, et on continue jusqu’à ce que tous les noeuds soient coloriés, ou qu’on ne puisse plus backtracker (et on est alors malheureusement tombé sur une instance insoluble du problème).
En Python, on peut implémenter cette procédure de la manière suivante :
couleurs = ["white",
"blue", "red", "green",
"orange", "yellow", "pink",
"cyan", "purple", "grey"]
def colorier_graphe(graphe):
# noeuds est une liste d'éléments (nom du noeud, couleur du noeud)
# aretes est une matrice d'adjacence
noeuds, aretes = graphe
nn = len(noeuds)
# Propriété "couleurs interdites" pour les noeuds
# vide pour le moment (qui contiendra des couples (couleur, noeud voisin);
# garder le noeud d'où provient la contrainte nous permettra de backtracker)
# On convertit les couleurs en nombres pour faciliter les comparaisons
sommets = [[x[0], couleurs.index(x[1]), []] for x in noeuds]
# Garder une trace des noeuds déjà coloriés
est_colorie = [False for i in range(nn)]
noeud_colorie_indices = []
for i in range(nn):
# 0 est non colorié
if (not(sommets[i][1] == 0)):
noeud_colorie_indices.append(i)
est_colorie[i] = True
sommets = backtracking_colorier(est_colorie, sommets, aretes, noeud_colorie_indices)
if (sommets == "BACKTRACKING"):
return("Insoluble")
noeuds = [[x[0], couleurs[x[1]]] for x in sommets]
return([noeuds, aretes])
def backtracking_colorier(est_colorie, sommets, aretes, noeud_colorie_indices):
nn = len(sommets)
from math import sqrt
nb_couleurs = int(sqrt(nn))
# S'il existe des noeuds dont la couleur doit être propagée
while (len(noeud_colorie_indices) > 0):
noeud_indice = noeud_colorie_indices.pop()
couleur = sommets[noeud_indice][1]
# Propagation de la contrainte sur
# la couleur aux voisins du noeud
for i in range(nn):
if (aretes[i][noeud_indice]):
# Alors le noeud d'indice i est un voisin du
# noeud d'indice noeud_indice
# On met à jour sa propriété "couleurs interdites"
sommets[i][2] += [[couleur, noeud_indice]]
# Si tous les noeuds sont coloriés
# retourner l'ensemble des sommets et leurs couleurs
if (all(est_colorie)):
return(sommets)
# Sinon, on considère un noeud non colorié
# (on recherche le premier indice tel que l'élément
# correspondant ne soit pas colorié
# Tous les noeuds ont au moins une couleur disponible
# sinon, on aura retourné une exception avant
noeud_non_colorie_indice = est_colorie.index(False)
couleurs_interdites = [paire[0] for paire in sommets[noeud_non_colorie_indice][2]]
couleurs_disponibles = filter(lambda x: not(x in couleurs_interdites), range(1, nb_couleurs+1))
# Si le noeud ne peut être colorié
if (len(couleurs_disponibles) == 0):
return("BACKTRACKING")
# Sinon on le colorie par une couleur disponible
couleur_choisie = min(couleurs_disponibles)
est_colorie[noeud_non_colorie_indice] = True
sommets[noeud_non_colorie_indice][1] = couleur_choisie
noeud_colorie_indices = [noeud_non_colorie_indice]
res = backtracking_colorier(est_colorie, sommets, aretes, noeud_colorie_indices)
# Backtracking
if (res == "BACKTRACKING"):
# On ajoute la couleur actuelle du noeud à la liste des couleurs interdites
couleurs_interdites = sommets[noeud_non_colorie_indice][2]
sommets[noeud_non_colorie_indice][2] += [[sommets[noeud_non_colorie_indice][1], "backtracking"]]
# On "décolorie" le noeud
sommets[noeud_non_colorie_indice][1] = 0
est_colorie[noeud_non_colorie_indice] = False
# On annule les contraintes sur ses voisins
# (d'où l'intérêt de conserver le noeud voisin qui donne la contrainte)
for i in range(nn):
if (aretes[i][noeud_non_colorie_indice]):
sommets[i][2] = filter(lambda paire:not(paire[1]==noeud_non_colorie_indice), sommets[i][2])
# Et on recommence !
return(backtracking_colorier(est_colorie, sommets, aretes, noeud_colorie_indices))
else:
return(res)
Exemples
Appliquons ce programme au problème 4 x 4 de la section précédente (les zéros dénotent les cases à compléter) :
sudoku44 = [
[0, 0, 3, 4],
[0, 4, 2, 1],
[0, 0, 0, 3],
[1, 3, 4, 2]
]
La solution (que vous auriez facilement trouvée par vous-même) est :
solution44 = [
[2, 1, 3, 4],
[3, 4, 2, 1],
[4, 2, 1, 3],
[1, 3, 4, 2]
]
En appliquant l’algorithme précédent, on obtient le graphe colorié suivant :
graphe = construire_graphe(sudoku44)
graphe = colorier_graphe(graphe)
grille = reconstruire_grille(graphe)
construire_graphe(grille)
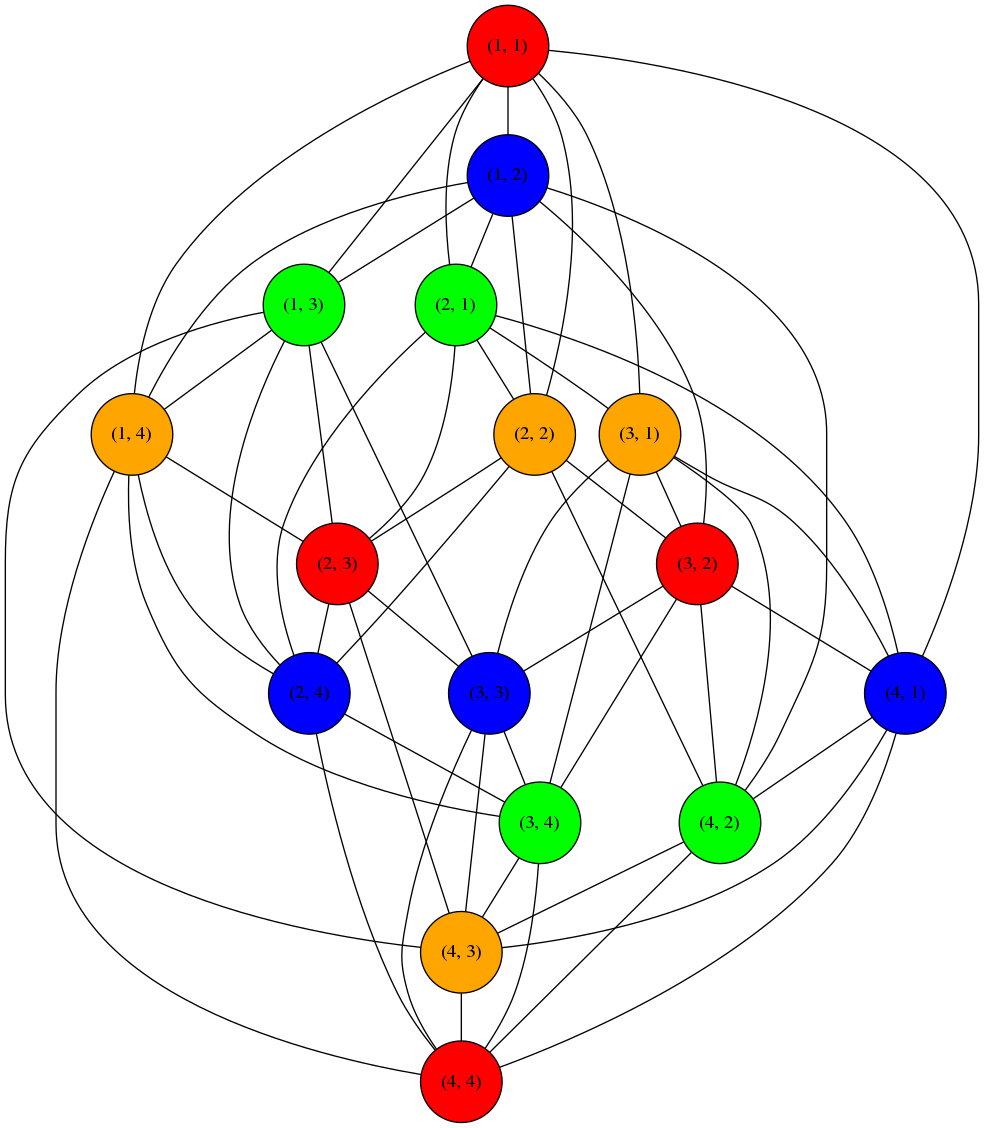
En convertissant cette solution en grille complète de sudoku, on obtient :
[
[2, 1, 3, 4],
[3, 4, 2, 1],
[4, 2, 1, 3],
[1, 3, 4, 2]
]
Qui est la même que la solution que nous avons trouvée manuellement.
Appliquons le programme maintenant au problème 9 x 9 :
exemple = [
[8, 0, 4, 9, 0, 3, 0, 7, 1],
[6, 3, 5, 8, 0, 7, 0, 2, 4],
[7, 1, 9, 0, 2, 4, 0, 5, 0],
[0, 8, 7, 0, 9, 1, 3, 0, 6],
[1, 0, 0, 7, 3, 6, 0, 0, 9],
[3, 0, 6, 4, 8, 0, 2, 1, 0],
[0, 6, 0, 5, 4, 0, 7, 3, 8],
[4, 7, 0, 3, 0, 2, 1, 9, 5],
[9, 5, 0, 1, 0, 8, 4, 0, 2]
]
graphe = construire_graphe(exemple)
graphe = colorier_graphe(graphe)
grille = reconstruire_grille(graphe)
construire_graphe(grille)
Le graphe obtenu est horrible. Vous pouvez vous faire “”"”plaisir”””” à le visualiser avec les fonctions décrites à la fin de cet article.
En convertissant cette solution en grille complète de sudoku, on obtient :
[
[8, 2, 4, 9, 5, 3, 6, 7, 1],
[6, 3, 5, 8, 1, 7, 9, 2, 4],
[7, 1, 9, 6, 2, 4, 8, 5, 3],
[5, 8, 7, 2, 9, 1, 3, 4, 6],
[1, 4, 2, 7, 3, 6, 5, 8, 9],
[3, 9, 6, 4, 8, 5, 2, 1, 7],
[2, 6, 1, 5, 4, 9, 7, 3, 8],
[4, 7, 8, 3, 6, 2, 1, 9, 5],
[9, 5, 3, 1, 7, 8, 4, 6, 2]
]
La fonction suivante en Python peut tester si cette solution respecte les règles du sudoku à notre place :
# On teste si une liste a des répétitions
# en testant si la longueur de la liste
# en entrée est égale à la longueur de la
# la liste dans laquelle on a supprimé
# toutes les répétitions
def est_unique(liste):
sans_repetitions = list(set(liste))
return(len(liste) == len(sans_repetitions))
# On teste si la solution respecte les
# règles du grille
# On suppose que toutes les valeurs de la grille
# sont comprises entre 1 et 9
def tester_solution(grille):
nb_lignes = len(grille)
# Toutes les lignes ont la même longueur
nb_colonnes = len(grille[0])
nb_sous_grilles = len(grille)
# ex. 9 pour une grille de taille 9 x 9
colonnes = []
for j in range(nb_colonnes):
colonne = []
# On met dans la même colonne
# tous les éléments à la position j
# dans chaque ligne
for i in range(nb_lignes):
colonne.append(grille[i][j])
# On ajoute la colonne à la liste des colonnes
colonnes += [colonne]
# Construire les sous-grilles de taille (racine carré de la
# taille de la grille initiale), qu'on note r
# La sous-grille qui commence à la ligne i
# et la colonne j (le coefficient en haut à gauche est
# la position (i,j)) comporte les coefficients
# aux positions (i, j), (i, j+1), (i, j+2), ..., (i, j+r-1)
# (i+1, j), (i+1, j+1), (i+1, j+2), ..., (i+1, j+r-1)
# (i+2, j), (i+2, j+1), (i+2, j+2), ..., (i+2, j+r-1)
# ...
# (i+r-1, j), ..., (i+r-1, j+r-1)
# Attention à l'indexage en Python qui commence à zéro !
sous_grilles = []
from math import sqrt
r = int(sqrt(len(grille)))
indices_depart = [r*i for i in range(r)]
for i in indices_depart:
for j in indices_depart:
# Le coefficient de départ est (i, j)
sous_grille = []
for k in [i+ui for ui in range(r)]:
for l in [j+uj for uj in range(r)]:
sous_grille.append(grille[k][l])
sous_grilles += [sous_grille]
# pour chaque ligne, on teste
# s'il y a des répétitions
for i in range(nb_lignes):
if (not est_unique(grille[i])):
return(False)
# pour chaque colonne
for i in range(nb_colonnes):
if (not est_unique(colonnes[i])):
return(False)
# pour chaque sous-grille
for i in range(nb_sous_grilles):
if (not est_unique(sous_grilles[i])):
return(False)
# Sinon, toutes les conditions ont été remplies
return(True)
tester_solution(grille)
> True
Pour aller plus loin
Comment est-on sûrs que l’algorithme (celui avec le backtracking) termine ? En fait, on énumère des “chemins”, où l’étape n est la couleur sélectionnée pour le nième noeud observé (dans cet algorithme, on inspecte les noeuds de gauche à droite, de haut en bas dans la grille). Le tableau “couleurs_disponibles” calculé pour chaque noeud observé donne les possibilités à explorer pour l’étape associée (comme un embranchement pour un véritable chemin). A chaque backtracking, on élimine une possibilité (on a exploré cette direction dans l’embranchement, et elle nous a mené à une impasse). Au final, on énumère les chemins possibles, jusqu’à trouver celui qui nous permet de trouver une solution pour chaque étape -ou alors, on a fini par explorer tous les chemins possibles, et aucun n’a abouti (le cas “Insoluble” dans l’algorithme).
Bon, je vous ai donné la solution sans trop me justifier. Ce serait bien de vérifier qu’effectivement, il est utile de chercher à résoudre le problème de coloriage de graphe pour faire des sudokus. En fait, le problème de sudoku, et ce problème de coloriage de graphe sont équivalents; autrement dit, si on trouve la solution pour une instance concrète de l’un de ces deux problèmes, on peut la convertir en solution de l’autre problème, après transformation de l’instance du premier problème en instance du second problème (par exemple, en convertissant la grille de sudoku en graphe) :
- Par exemple, si on trouve une solution à la grille de sudoku, on convertit alors cette grille en graphe (comme expliqué précédemment), et on colorie chaque noeud du graphe selon la valeur de la case correspondante. Comme toutes les valeurs d’une ligne (respectivement, colonne ou sous-grille) sont différentes (ce sont les conditions pour une solution de grille de sudoku), alors tous les noeuds correspondants auront une couleur distincte, ce qu’on voulait dans le problème de coloriage de graphe (en utilisant la définition de voisinage que l’on s’est choisie).
- Inversement, si on a une solution pour le problème de coloriage, alors on convertit le graphe colorié résultant à nouveau en grille de la façon suivante : on remplace chaque couleur de noeuds par une valeur distincte (entre 1 et 9), et, si on a conservé les positions de cases associées à chaque noeud du graphe, on positionne les valeurs des cases dans les positions correspondantes. Les valeurs sont distinctes entre noeuds voisins (ce qui est la condition pour une solution du problème de coloriage), donc, en utilisant à nouveau la définition de voisinage, toutes les valeurs obtenues sont uniques par ligne, colonne et sous-grille. On obtient alors bien une solution de grille de sudoku.
En gage de bonne foi, voilà le code Python correspondant à ces transformations :
# Créer le graphe et produire une image PNG
# en utilisant GraphViz, que vous pouvez aussi voir
# dans la boîte à outils de Tryalgo
# (http://tryalgo.org/toolbox/)
def construire_graphe(grille):
from subprocess import call
couleurs_cases = couleurs[:len(grille)+1]
filename="sudoku" + str(len(grille))*2
sudoku = "graph {\n"
# Dimension de la grille
n = len(grille)
# Liste de noms et couleurs de noeuds
noeuds = []
# Le coefficient d'indice (i, j) est à la position n*i+j
# dans la liste noeuds
for i in range(n):
for j in range(n):
nom = "\"(" + str(i+1) + ", " + str(j+1) + ")\""
couleur = couleurs_cases[grille[i][j]]
noeuds.append([nom, couleur])
# Ajouter le noeud au fichier DOT
sudoku += "node [style=filled fillcolor=" + couleur
sudoku += " shape=circle]\n"
sudoku += nom + ";\n"
# Matrice d'adjacence pour le graphe
# aretes[i][j] = True si et seulement si le noeud i
# et le noeud j sont voisins
aretes = [[False]*(n*n) for j in range(n*n)]
for i in range(n):
for j in range(n):
for k in range(n):
# Voisinage par ligne
aretes[n*i+j][n*i+k] = True
# Voisinage par colonne
aretes[n*i+j][n*k+j] = True
# Voisinage par sous-grille
# Remarquer que toutes les positions de
# coefficients d'une même sous-grille
# (numéros de ligne et de colonne)
# ont le même quotient q pour la division
# euclidienne par r, où r est
# la racine carré de la taille de la
# grille initiale
# (voir le commentaire de la fonction
# est_unique)
from math import sqrt
r = int(sqrt(n))
# Valeurs de quotient
q_i, q_j = int(i/r), int(j/r)
# On énumère les valeurs possibles de reste
# 0, 1, 2, ..., r-1
for reste_i in range(r):
for reste_j in range(r):
# Enumérer les coordonnées de noeuds (ii, jj)
ii = r*q_i+reste_i
jj = r*q_j+reste_j
aretes[n*i+j][n*ii+jj] = True
# On ne met pas de boucle élémentaire
# autrement dit, d'arête d'un noeud vers lui-même
for i in range(n*n):
# Pour éviter de mettre une boucle élémentaire
# et parce que la matrice d'adjacence est ici symétrique
# (le graphe est non orienté)
for j in range(i+1, n*n):
if (aretes[i][j]):
sudoku += noeuds[i][0] + " -- " + noeuds[j][0] + ";\n"
aretes[i][i] = False
graphe = [noeuds, aretes]
sudoku += "}"
# On crée le fichier DOT associé au graphe
with open(filename+".dot", "w") as f:
f.write(sudoku)
# Conversion du fichier DOT en image PNG
call("dot -Tpng " + filename + ".dot > " + filename + ".png", shell=True)
return(graphe)
def reconstruire_grille(graphe):
noeuds, aretes = graphe
from math import sqrt
# On a n^2 cases, où n est la taille de la grille
n = int(sqrt(len(noeuds)))
grille = []
for i in range(n):
ligne = []
for j in range(n):
couleur = noeuds[n*i+j][1]
# Retrouve l'indice de l'élément couleur
# dans le tableau couleurs
valeur = couleurs.index(couleur)
ligne.append(valeur)
# On met la ième ligne dans la grille
grille += [ligne]
return(grille)
Référence (en anglais)
“Sudoku Game Solution Using Graph Coloring” de Bharathi Dharavath