Solutions du Google Hash Code 2017 - Streaming Videos

Feb 27, 2017 • Christoph Dürr, Jill-Jênn Vie et Finn Völkel

Nous décrivons ici notre petite expérience avec le concours Google Hashcode 2017 : Optimize Cache Servers for YouTube.

Le problème Streaming Videos

On vous donne une liste de fichiers vidéos avec chacun une taille. Puis il y a un graphe biparti entre des caches d’une part et des terminaux d’autre part. Les arêtes sont étiquetées par une latence. Tous les caches ont la même capacité et peuvent contenir des fichiers vidéos. Plusieurs copies d’une vidéo peuvent être déployés dans les caches. Il existe un serveur central contenant tous les vidéos, connecté à tous les terminaux, chacune des connexions ayant une latence distincte. Quand un terminal doit accéder à une vidéo, il se connecte au cache adjacent qui minimise la latence de la connexion, et en dernier recours il se connecte au serveur central. Et finalement pour chaque vidéo et chaque terminal il existe un nombre de demandes de connexion. Le score d’un placement de vidéos dans les caches est défini comme la latence moyenne sur toutes les demandes de vidéos. Le but est essentiellement de minimiser ce score.

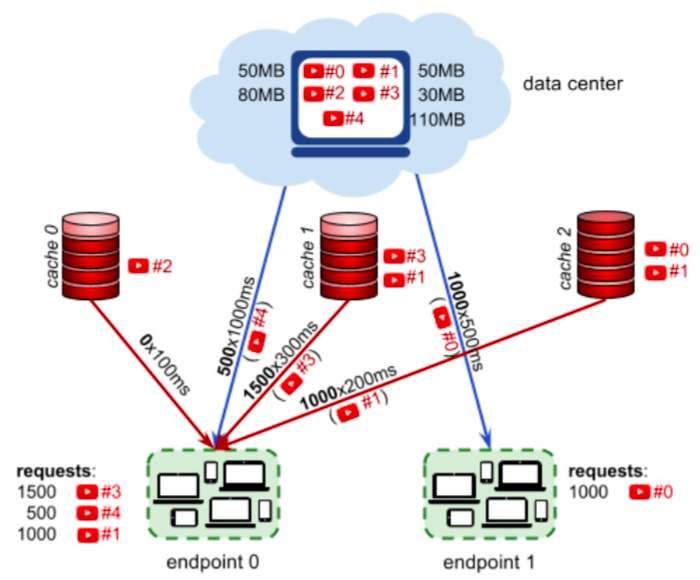
Les instances

$V$ = nombre de vidéos
$E$ = nombre de terminaux
$R$ = nombre de requêtes (pas important dans l’estimation de la complexité)
$C$ = nombre de caches
$X$ = capacité des caches (pas important dans l’estimation de la complexité, sauf si on considère aussi la taille moyenne des vidéos)

instance	V	E	R	C	X
kittens.in	10000	1000	200000	500	6000
me_at_the_zoo.in	100	10	100	10	100
trending_today.in	10000	100	100000	100	50000
videos_worth_spreading.in	10000	100	100000	100	10000

Ces valeurs permettent d’estimer les temps de calcul pour différents algorithmes auxquels on pourrait penser.

Une solution gloutonne

En plaçant les vidéos dans les caches de manière gloutonne on arrive à des scores dans les 800 000. En jouant sur des priorités de traitement sur les vidéos et les terminaux, on peut déjà monter à un score de 2 100 000. Jill-Jênn a écrit une telle solution particulièrement courte (2 098 124 points) :

score = Counter()
for r in requests:
    for i_cache in to_cache[r.endpoint]:
        # Si on mettait la vidéo requise dans le cache i, combien aurait-on de points ?
        score[(r.video, i_cache)] += (to_data[r.endpoint] - to_cache[r.endpoint][i_cache]) * r.nb
contained = [[] for _ in range(C)]
done = [False] * V
for (i_video, i_cache), _ in score.most_common():
    if not done[i_video] and sum(size[v] for v in contained[i_cache]) + size[i_video] <= X:
        # Si on ne dépasse pas, le faire (on choisit un unique cache pour chaque vidéo pour commencer)
        contained[i_cache].append(i_video)
        done[i_video] = True
for (i_video, i_cache), _ in score.most_common():
    if not i_video in contained[i_cache] and sum(size[v] for v in contained[i_cache]) + size[i_video] <= X:
        # On remplit le rab de cache si possible
        contained[i_cache].append(i_video)
# Enfin, on affiche la solution obtenue
print(C)
for i_cache in range(C):
    print(i_cache, ' '.join(map(str, contained[i_cache])))

L’algorithme glouton suivant permet d’atteindre des bons gains. Pour une solution donnée (initialement tous les caches sont vides) on peut associer une efficacité à toute paire (cache $c$, vidéo $v$). Tout simplement on calcule l’augmentation de la valeur objectif qu’apporterait un placement de la vidéo $v$ dans le cache $v$. Pour cela, il faut boucler sur tous les terminaux $e$ dont une requête pour $v$ émane et qui sont connectés à $c$. Cette augmentation est alors divisée par la taille de la vidéo pour constituer l’efficacité de la paire $(c,v)$. L’algorithme glouton cherche alors à placer $v$ en $c$ pour toutes les paires $(c,v)$ par ordre décroissant d’efficacité. Le calcul de l’efficacité était coûteux — $O(CVE)$ pour être précis — il est effectué seulement à des intervalles réguliers, en fait dès que la charge totale des caches a augmenté d’un millième.

Une recherche locale par résolution de sac à dos

On peut améliorer une solution existante de la manière suivante. Pour un cache fixé $c$, on le vide complètement. Puis pour chaque vidéo $v$, on détermine le gain en score que représenterait la présence de $v$ dans le cache $c$. Ceci se fait en temps $O(EVC)$, où $E$ est le nombre de terminaux, $V$ le nombre de vidéos et $C$ le nombre de caches. Ainsi toute vidéo a un gain et une taille. Et on résout de manière exacte le problème de sac à dos consistant à trouver un ensemble de vidéos de taille totale au plus la capacité du cache et de gain total maximum. Ceci se fait par programmation dynamique en temps $O(VX)$ où $X$ est la capacité du cache.

Notre solution consiste alors à appliquer cette amélioration sur tous les caches, de manière répétée, jusqu’à ce que le score n’augmente plus. Avec cette approche on obtient un score dans les 2 500 000.

Solutions

L’entrée trending today a pu ainsi être résolue d’une manière optimale, nous semble-t-il. C’est l’instance la plus coûteuse en temps (de l’ordre d’une heure), mais en une seule itération un point fixe a été atteint (rapidement détectée en une seconde par une deuxième itération). Cette instance a tellement de structure, de symétrie, qu’une autre solution semble possible.

On aurait pu imaginer une solution gloutonne, où chaque terminal demande à placer les vidéos les plus demandées dans son cache le plus proche.

Les entrées me at the zoo et videos_worth_spreading sont résolues rapidement, en quelques secondes pour la première et de l’ordre de 5 minutes pour la deuxième. Le traitement de kittens prend par contre beaucoup de temps. On appelle une itération l’amélioration de chacun des caches. Pour cette entrée, chaque itération prend environ 13 minutes, pour un total de 3 à 4 heures. En revanche, après la première itération le score est déjà à 99 % du score final, lorsque le point fixe est atteint.

L’implémentation

La solution de Christoph et Finn a été implémentée en C++ et exécutée sur un PC GNU/Linux avec processeur à 2,6 GHz.

La solution de Jill-Jênn a été implementée en Python et renvoie la sortie de kittens (la plus coûteuse) en 1 min 15 sur un Mac avec Core i5 1,3 GHz, à condition d’utiliser pypy3.

Amélioration des techniques

Nous avons observé que sur certains fichiers d’entrée, seules 15 % des vidéos avaient un gain positif. Alors nous avons restreint notre instance du problème de sac à dos à seulement ces vidéos.

Nous avons tenté une approche top-down de programmation dynamique, mais l’utilisation d’un dictionnaire a plutôt ralenti l’exécution.

Nous avons également tenté d’améliorer le calcul du gain des vidéos en maintenant pour chaque paire terminal-vidéo l’indice du cache le plus proche contenant cette vidéo. Mais l’amélioration ne s’est pas fait ressentir. Dommage, pour tellement de changements de code.

À chaque itération nous avons traité les caches dans un ordre aléatoire différent. Par contre, nous n’avons pas testé si cela améliorait l score. Il semblait que pour différentes initialisations de la source d’aléa les résultats étaient identiques pour le jeu de données me at the zoo.

Pour boucler rapidement sur les terminaux, qui pourraient demander une vidéo $v$ dans un cache $c$, nous avons préparé deux listes: $c2e[c]$ donne les terminaux connectés à $c$, et $v2e[v]$ les terminaux dont une requête existe pour la vidéo $v$. Ensuite il suffit de boucler sur la plus petite des deux listes, comme ceci :

vector<int> c2e [MAX_C];
vector<int> v2e [MAX_V];
// ...
    vector<int> & e_list = (v2e[v].size() < c2e[c].size()) ? v2e[v] : c2e[c];
    for (int e: e_list)

Conclusion

Il nous semble qu’une approche générale gagnante pourrait être constituée d’une première solution obtenue par un algorithme glouton, suivi d’une recherche locale. Les scores que nous avons obtenus (dans le Extended Round) sont assez proches des meilleures solutions (à 97 %). Une stratégie pourrait être que les différents membres d’une équipe écrivent chacun un programme qui donne de bonnes solutions pour une instance particulière, permettant d’exploiter les spécificités de chacune.

Nous restons très impressionnés des scores obtenus par les meilleures équipes dans la période assez courte du concours, comme par exemple Bibeleskaes de l’université de Strasbourg. L’équipe de l’ENS Paris-Saclay a quant à elle été 5e équipe française sur 465.

À bientôt pour un autre concours ! En attendant n’hésitez pas à vous entraîner.

.@UnivParisSaclay des liENS classée 5e sur 465 équipes françaises au Google #HashCode yaaay!!! #purjeudemots pic.twitter.com/QV8HS3ljAz
— Jill-Jênn Vie (@jjvie) 23 février 2017