Qualifications Facebook Hacker Cup 2017
Pour commencer l’année, ce week-end de l’épiphanie ont eu lieu les qualifications de Facebook Hacker Cup.
Progress Pie
Il fallait dire, pour un certain pourcentage d’un camembert de progression, si un certain pixel devait être noir ou blanc.
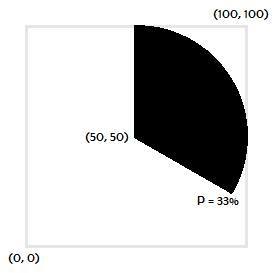
Astuce. Comme c’est pénible de faire le passage de clockwise à counter-clockwise au niveau du calcul de l’angle, autant inverser X et Y pour s’intéresser à la symétrie de la figure par rapport à $y = x$ et ainsi directement avoir la correspondance pourcentage et angle !
La fonction atan2(dy, dx) renvoie la valeur de l’angle (arctan) pour des mesures algébriques dy, dx (i.e., des différences de coordonnées).
from math import atan2, pi, sqrt
def dist2(x, y):
return pow(x - 50, 2) + pow(y - 50, 2)
T = int(input())
for t in range(T):
P, X, Y = map(int, input().split())
percent = atan2(X - 50, Y - 50) / (2 * pi)
if P > 0 and 100 * percent <= P and dist2(X, Y) <= 50 * 50:
print('Case #%d: black' % (t + 1))
else:
print('Case #%d: white' % (t + 1))Pitfall. Je me suis fait avoir par la ligne suivante de l’énoncé :
When the progress percentage, P, is greater than 0%, a sector of angle (P% * 360) degrees is colored black
Il faut en effet faire un cas particulier lorsque $P = 0$ puisque rien n’est censé être dessiné, pas même une seule ligne noire. D’où le if P > 0 and dans le code.
Lazy Loading
Un glouton suffit.
from math import ceil
T = int(input())
for t in range(T):
N = int(input())
w = []
for _ in range(N):
w.append(int(input()))
w.sort()
nb_carried = 0
nb_trips = 0
while nb_carried < N:
nb_trips += 1
heaviest = w.pop()
nb_carried += ceil(50 / heaviest)
if nb_carried > N:
nb_trips -= 1
print('Case #%d: %d' % (t + 1, nb_trips))Fighting the Zombie
Quelle est la probabilité que la somme de $k$ dés à $f$ faces comprises entre $a$ et $a + f - 1$ soit supérieure ou égale à un certain $h$ ?
Au départ j’ai cru que je pourrais tricher avec la bibliothèque Python lea de distributions de probabilités discrètes faite par Pierre Denis.
from lea import V, Pf
import re
def sum_dice(nb_samples, nb_faces, sign=None, shift=None):
start = 1
if sign:
start += (-1 if sign == '-' else 1) * int(shift)
return sum(V(*range(start, start + int(nb_faces))) for _ in range(int(nb_samples)))
T = int(input())
for t in range(T):
H, S = map(int, input().split())
dices = input().split()
winnings = []
for dice in dices:
m = re.match(r'^([0-9]+)d([0-9]+)([+-])?([0-9]+)?$', dice)
nb_samples, nb_faces, sign, shift = m.groups()
draw = sum_dice(nb_samples, nb_faces, sign, shift)
winnings.append(Pf(draw >= H))
print('Case #%d: %f' % (t + 1, max(winnings)))Ce Pf(draw >= H) est en outre scandaleusement sucré syntaxiquement :D
Mais y a beaucoup d’outcomes possibles lorsqu’on somme 20 dés 6. Donc plutôt que de calculer les convolutions successives (avec numpy.convolve par exemple) il vaut mieux passer par les fonctions génératrices, comme exprimé dans ce post Mathematics Stack Exchange ou ce post de blog d’un consultant en statistiques qui a 4 enfants :
from numpy.polynomial.polynomial import polypow
from numpy import ones
import re
# Code éhontément pompé de http://www.johndcook.com/blog/2013/04/29/rolling-dice-for-normal-samples-python-version/,
# comme sans doute pour 90 % des candidats Python à Hacker Cup 2017
def proba_sum_dice(nb_samples, nb_sides, sign, shift, greater_than):
if sign:
greater_than -= (-1 if sign == '-' else 1) * int(shift)
# Create an array of polynomial coefficients for
# x + x^2 + ... + x^sides
p = ones(nb_sides + 1)
p[0] = 0
# Extract the coefficients of p(x)**dice and divide by sides**dice
pmf = nb_sides**(-nb_samples) * polypow(p, nb_samples)
cdf = pmf.cumsum()
if greater_than - 1 >= len(cdf):
return 0
if greater_than - 1 < 0:
return 1
return 1 - cdf[greater_than - 1]
T = int(input())
for t in range(T):
H, S = map(int, input().split())
dices = input().split()
winnings = []
for dice in dices:
m = re.match(r'^([0-9]+)d([0-9]+)([+-])?([0-9]+)?$', dice)
nb_samples, nb_sides, sign, shift = m.groups()
winnings.append(proba_sum_dice(int(nb_samples), int(nb_sides), sign, shift, greater_than=H))
print('Case #%d: %f' % (t + 1, max(winnings)))Notez la regexp scandaleuse pour parser les XdY±Z.
À bientôt, et n’oubliez pas que ce maudit concours ne tolère qu’une soumission par problème. Voir la liste des autres concours de programmation.
