Skip to main content Link Search Menu Expand Document (external link)
    

Debuggue mon flot max (si t'es cap)

Pourquoi sur le graphe de capacités suivantes :

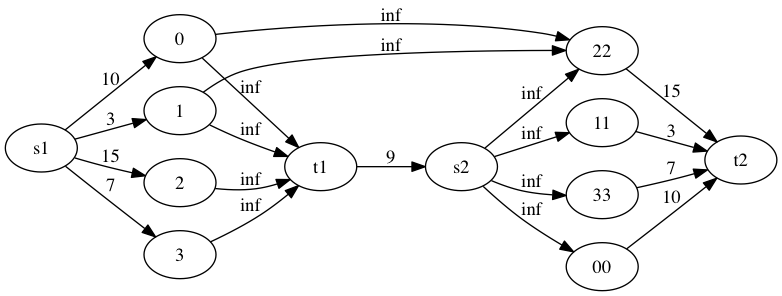
J’obtiens un flot max à 13 :

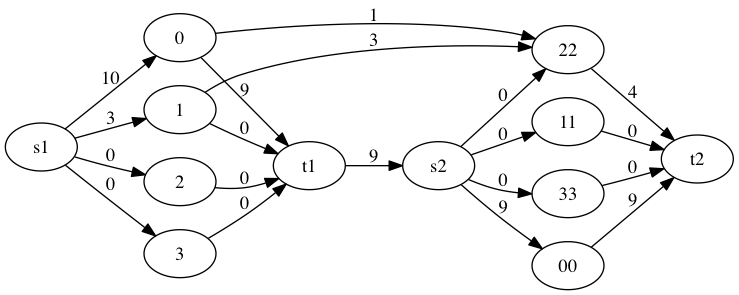o

Alors qu’il en existe un à 22 :

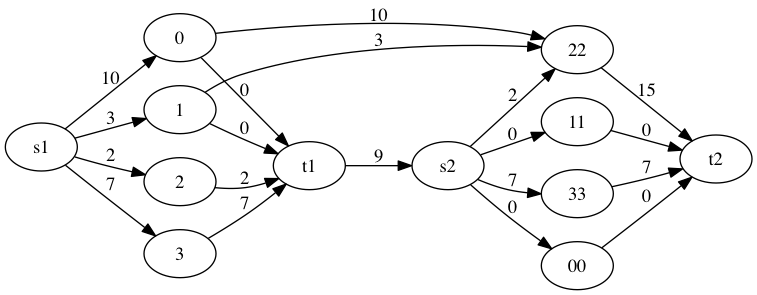
J’ai l’impression que c’est parce qu’il existe un chemin augmentant qui emprunte l’arête inverse t1 <- 0. Mais du coup, faut-il considérer une « capacité négative » sur cet arc ? Est-ce que ça a du sens ?

Voici le code, B.cpp :

#include <iostream>

#include <vector>

#include <unordered_map>

using namespace std;

#define SIZE 2 * 100 + 4
#define INF 1e9

int n, m;
bool visit[SIZE];
vector<int> graph[SIZE];
unordered_map<int, int> capacity, flow;

int c = 0;

bool augment(int u, int val) {
    c++;
    // cout << "-> " << u << " " << val << endl;

    visit[u] = true;
    if(u == 2 * n + 3)
        return val;
    int v, res, delta, cuv;
    for(int i = 0; i < graph[u].size(); ++i) {
        v = graph[u][i];
        cuv = capacity[u * SIZE + v];
        if(!visit[v] && cuv > flow[u * SIZE + v]) {
            res = min(val, cuv - flow[u * SIZE + v]);
            delta = augment(v, res);
            if(delta > 0) {
                flow[u * SIZE + v] += delta;
                flow[v * SIZE + u] -= delta;
                return delta;
            }
        }
    }
    return 0;
}

void graphviz() {
    cout << "digraph G {" << endl << "rankdir=LR;" << endl;
    int v;
    for(int u = 0; u < 2 * n + 4; ++u) {
        for(int i = 0; i < graph[u].size(); ++i) {
            v = graph[u][i];
            cout << u << " -> " << v << "[label=" << flow[u * SIZE + v] << "];" << endl;
        }
    }
    cout << "}" << endl;
}

void add(int u, int v, int c) {
    graph[u].push_back(v);
    flow[u * SIZE + v] = 0;
    flow[v * SIZE + u] = 0;
    capacity[u * SIZE + v] = c;
}

int main() {
    int nbTests;
    int clean[100][100];
    int a[100], b[100], s[100];
    cin >> nbTests;
    for(int t = 1; t <= nbTests; ++t) {
        cin >> n >> m;
        for(int i = 0; i < n; ++i)
            cin >> a[i] >> b[i] >> s[i];
        for(int i = 0; i < n; ++i)
            for(int j = 0; j < n; ++j)
                cin >> clean[i][j];
        int s1 = 2 * n, t1 = 2 * n + 1, s2 = 2 * n + 2, t2 = 2 * n + 3;
        for(int i = 0; i <= t2; ++i)
            graph[i].clear();
        for(int i = 0; i < n; ++i) {
            // cout << i << ": " << s[i] << " " << ceil(s[i] / m) << endl;

            add(s1, i, ceil(s[i] / m));
            add(i, t1, INF);
            add(s2, n + i, INF);
            add(n + i, t2, ceil(s[i] / m));
        }
        for(int i = 0; i < n; ++i)
            for(int j = 0; j < n; ++j)
                if(b[i] + clean[i][j] <= a[j])
                    add(i, n + j, INF);
        add(t1, s2, 9);
        if(t == 2) {
            do {
                for(int i = 0; i <= t2; ++i)
                    visit[i] = false;
            } while(augment(s1, 1e9) > 0);
            graphviz();
        }
    }
    // graphviz();

    /* int d = 1;
    
    for(int i = 0; i < n; ++i) {
        if(flow[2 * n * SIZE + i] < 1) {
            cout << "NO" << endl;
            // cout << c << " " << d << endl;
            return 0;
        }
    }
    cout << "YES" << endl;
    cout << c << " " << d << endl; */
    return 0;
}

Sur l’entrée suivante, B.in :

1
4 1
1 100 10
50 130 3
150 200 15
80 170 7
0 2 3 4
5 0 7 8
9 10 0 12
13 14 15 0

Commentaires

Sujets similaires