Comment marche l'outil "Seau" de Paint ?
Contexte
Le titre se suffit à lui-même. Ssh. Ne vous inquiétez pas. Personne ne vous jugera pour ne (jamais) vous être posé la question.
Pour rappeler ce qu’est cet outil pour les néophytes en graphisme, l’outil “Seau” (ou outil de remplissage, selon le logiciel) est une fonctionnalité qui permet de colorier tous les pixels de la même couleur que celui que vous avez sélectionné sur votre image avec la couleur courante. Par exemple, si jamais vous avez tenté de faire une carte maison pour la Saint Valentin, et que vous n’aviez pas envie de vous amuser à colorier à la brosse les petits coeurs, vous avez pu utiliser cet outil (le curseur est marqué en vert ci-dessous; la couleur courante est ici le rouge) :
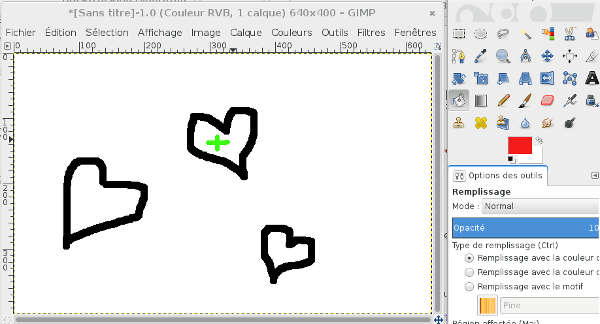

“Oh mon amour que c’est joli”, maintenant qu’on a fait le clin d’oeil à la Saint Valentin, on va pouvoir aux choses sérieuses. Genre, l’algorithme.
Une première idée (qui vous oriente dans la bonne direction)
Intuitivement, cet outil colorie avec la couleur courante tous les pixels contenus dans la figure délimitée par un changement de couleur. Si la feuille est de couleur uniforme (tous les pixels du fichier sont de la même couleur), tous les pixels sont alors coloriés. Si le pixel sélectionné par le curseur est d’une couleur différente de celle de ses voisins, c’est-à-dire les pixels à gauche, à droite, en haut et en bas, alors seulement le pixel sélectionné sera colorié.
L’analogie avec le pot de peinture devient alors plus claire (sinon évidente) : vous versez le pot de peinture sur le pixel sélectionné, et la peinture se propage sur les voisins du pixel, puis aux voisins de ces voisins, etc. Réfléchissons alors de manière algorithmique comment traduire cette action : on veut coder l’action de peindre, récursivement sur les voisins d’un pixel considéré, jusqu’à remplir une certaine condition d’arrêt (un changement de couleur, par exemple).
Formalisation du problème
Pas de panique, pas de mathématiques compliquées à l’horizon. Vous souvenez-vous des graphes introduits dans l’article sur l’algorithme de Dijkstra ? (Evidemment, me répondez-vous en choeur). Une feuille dans Paint (c’est-à-dire l’ensemble de pixels sur lequel vous pouvez gribouiller) peut être convertie en graphe non orienté. Chaque pixel est un noeud du graphe (auquel on associe une couleur, celle que le pixel considéré a actuellement sur la feuille). Deux pixels sont liés par une arête si et si seulement s’ils sont voisins.
A partir de ce moment, vous savez quoi faire. Etant donné la couleur courante et la couleur à remplacer par la couleur courante (celle du pixel sélectionné en premier lieu par le curseur), tant que le pixel que vous voyez est de la couleur à remplacer, vous changez sa couleur, puis vous énumérez les noeuds reliés à ce pixel et réappliquez la procédure à chacun d’entre eux. Une fois que l’algorithme est terminé, vous devez être sûrs que tous les pixels qui sont accessibles depuis le pixel initial et qui sont de la couleur à remplacer sont coloriés avec la couleur courante. Les noeuds accessibles depuis un noeud n donné sont tels qu’on puisse dessiner une ligne entre ces noeuds et le noeud initial en n’utilisant que des arêtes du graphe sans lever le crayon.
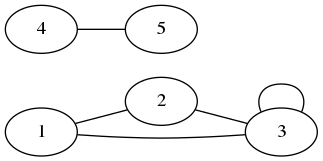
Par exemple, pour le graphe ci-dessus, les noeuds 2 et 3 sont accessibles depuis le noeud 1 (et réciproquement). Les noeuds 4 et 5 ne sont pas accessibles depuis le noeud 1.
Heureusement, on connaît des algorithmes qui énumèrent les noeuds accessibles depuis un noeud fixé (ce sont les parcours en profondeur et en largeur qui sont présentés dans la prochaine section). Et voilà, c’est bon, vous avez résolu le problème. Ecrivons toutefois pour de bon l’algorithme en Python.
Algorithme de remplissage par diffusion (ou “Flood Fill”)
L’algorithme n’utilise pas les raccourcis d’écriture de Python, pour plus de lisibilité.
# feuille est la feuille de travail de Paint, i.e. un graphe
# sous forme de listes d'adjacence (voir l'article sur Dijkstra)
# Un pixel est identifié par un entier et par une couleur
# i est l'identifiant du pixel initial
# courante est la couleur courante
def remplissage(feuille, i, courante):
# remplacer est la couleur à remplacer par la couleur
# courante (c'est la couleur du pixel initial)
# voisins est la liste d'identifiants entiers de
# pixels voisins du pixel initial i
[remplacer, voisins] = feuille[i]
# On remplace la couleur du pixel initial par la
# couleur courante
feuille[i] = [courante, voisins]
# On stocke les pixels accessibles depuis le noeud i
# qui sont potentiellement coloriés avec la couleur à remplacer
pixels_accessibles = voisins
# On note les pixels que l'on a déjà vu (pour ne pas
# se retrouver dans une boucle de traitement infinie...)
pixels_deja_vus = [False]*len(feuille)
# Tant que la liste de pixels à inspecter
# n'est pas vide (bonjour, c'est une pile)
while (len(pixels_accessibles) != 0):
# Retirer le premier pixel de la liste
p = pixels_accessibles[0]
# On note que l'on a vu ce pixel
pixels_deja_vus[p] = True
pixels_accessibles = pixels_accessibles[1:]
# Récupérer sa couleur et ses voisins
[c, v] = feuille[p]
if (c == remplacer):
# Changer sa couleur
feuille[p] = [courante, v]
voisins_a_ajouter = []
# On ajoute les voisins non vus de ce pixel
# dans la liste de pixels à inspecter
# puisque accessibles depuis le noeud initial
# et peut-être coloriés avec la couleur à remplacer
for voisin in v:
if (not pixels_deja_vus[voisin]):
pixels_accessibles = [voisin] + pixels_accessibles
# Et on itère !
# Comme on inspecte les pixels par ordre antichronologique
# d'ajout dans la liste (c'est-à-dire, les pixels vus en premier
# sont les pixels ajoutés le plus récemment dans la liste),
# on dit qu'on fait un parcours en profondeur des noeuds du graphe.
# Sinon, on fait un parcours en largeur des noeuds du graphe.
# (en remplaçant la ligne "pixels_accessibles = [voisin] + pixels_accessibles"
# par "pixels_accessibles += [voisin]")
# A cette étape, on a parcouru tous les pixels accessibles depuis le noeud initial
# et qui étaient de la couleur à remplacer
return(feuille)Exemples
Donnons-nous un exemple simple pour appliquer l’algorithme écrit précédemment (pas forcément très exaltant : vous pouvez voir des animations sur des exemples beaucoup plus intéressants ici par exemple). Il est de taille 3 pixels par 3. Les pixels blancs et rouges sont représentés sur une grille bordée de noir pour mieux les visualiser.

Convertissons-le en graphe comme expliqué précédemment.
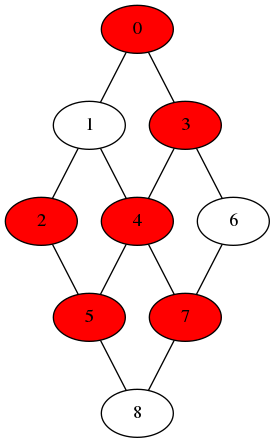
Supposons que l’on veuille colorier les pixels rouges en bleu, car les coeurs en rouge, c’est très surfait. On sélectionne le pixel numéroté 7.
feuille = [
["rouge", [1, 3]],
["blanc", [0, 2, 4]],
["rouge", [1, 5]],
["rouge", [0, 4, 6]],
["rouge", [1, 3, 5, 7]],
["rouge", [2, 4, 8]],
["blanc", [3, 7]],
["rouge", [6, 4, 8]],
["blanc", [5, 7]]
]
print(remplissage(feuille, 7, "bleu"))L’algorithme retourne :
> [
['bleu', [1, 3]],
['blanc', [0, 2, 4]],
['bleu', [1, 5]],
['bleu', [0, 4, 6]],
['bleu', [1, 3, 5, 7]],
['bleu', [2, 4, 8]],
['blanc', [3, 7]],
['bleu', [6, 4, 8]],
['blanc', [5, 7]]
]Ce à quoi on s’attendait.
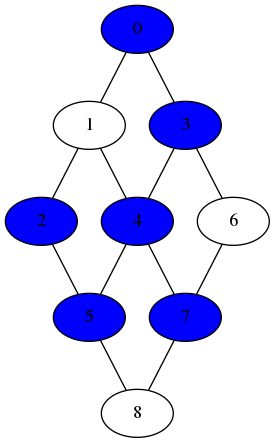
“Que c’est beauuu”
Pour aller plus loin
L’algorithme termine, car le nombre de pixels accessibles depuis le noeud initial et non vus décroît strictement à chaque itération de la boucle while.
La preuve de correction repose sur le fait que, si on considère la liste de tous les noeuds accessibles depuis le noeud initial coloriés avec la couleur à remplacer (en comptant le noeud initial), énumérés par un parcours en profondeur (respectivement, en largeur), à la fin de l’itération numéro k de la boucle while, les k+1 premiers noeuds de la liste sont coloriés avec la couleur courante (C’est donc une propriété de récurrence à démontrer). Pour k=0 (aucune itération de la boucle while), le noeud initial est colorié avec la couleur courante.
Il est à noter que, dans le cas de l’outil Paint, il y a au maximum quatre voisins pour chaque pixel. Mais bien sûr, la notion de voisin peut être modifiée, par exemple, pour décompter huit voisins (est, ouest, nord, sud, nord-est, nord-ouest, sud-est, sud-ouest), ou tout nombre arbitraire de voisins. Le principe de base de l’algorithme reste exactement le même.
Pour optimiser le temps de calcul de l’algorithme (surtout pour des feuilles de grande taille, donc avec beaucoup de pixels), et le stockage d’un possiblement très grand nombre de pixels à inspecter, on peut également modifier la structure de données (c’est-à-dire le type d’objet programmé) qui contient les voisins à une étape donnée, par exemple, pour éviter de prendre en compte des pixels déjà vus; ou changer de méthode d’énumération de voisins (en profondeur ou en largeur, si vous vous y connaissez un peu en graphes); ou exécuter l’algorithme de manière itérative plutôt que récursive (considérer la liste de voisins plutôt qu’appeler l’algorithme sur chaque voisin); ou décomposer en différentes méthodes la recherche de voisins. Le coeur de l’algorithme restant le même, il n’a pas été jugé utile d’en parler ici.
Ce qui est très intéressant dans cette méthode, c’est qu’elle est relativement simple à comprendre, et peut être utilisée pour des problèmes en apparence très éloignés du domaine du graphisme, par exemple, pour le jeu du démineur -quand vous cliquez sur une case qui n’est pas une bombe, et qui dévoile par conséquent d’autres cases- trouver un chemin vers la sortie dans un labyrinthe, ou la résolution de sudokus. Oui, vous avez bien lu. La résolution de sudokus. La suite au prochain épisode.