Rechercher des mots dans un texte par l'algorithme de Knuth-Morris-Pratt

Dec 11, 2016 • Clémence Réda

Contexte

La recherche des répétitions d’un morceau de texte (appelé motif) au sein d’un texte généralement plus long a de nombreuses applications concrètes. Pour n’en citer qu’une, la résolution de ce problème permet d’étudier soigneusement les séquences ADN en biologie. La rapidité d’exécution des algorithmes est d’autant plus importante que les données traitées sont souvent de taille conséquente…

On note M le motif recherché, contenant m lettres, et T le texte de n lettres dans lequel s’effectue la recherche. Pour formaliser le problème de manière générale, on cherche les indices de lettres i tels que, si T[k,l] est le mot commençant par la kième lettre de T (en numérotant à partir de 1) et finissant par la lième lettre de T, alors T[i,i+m-1] = M[1,m] = M. Pour simplifier la lecture, si jamais l<k, alors T[k,l] est par convention le mot ne comportant aucune lettre (“mot vide”).

Par exemple, dans l’image ci-dessous (chaque case des deux tableaux T et M contiennent des lettres), les cases coloriées en bleu sont des cases alignées dans M et T, i.e. chaque case de T en face d’une case de M contient la même lettre.

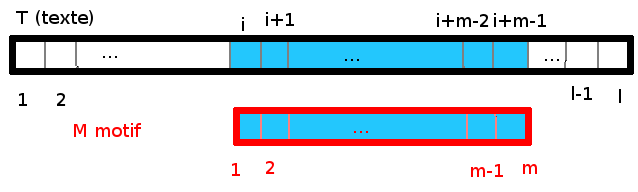
Un exemple concret

Votre rêve d’enfant s’est accompli -mais si- : vous voilà un écrivain (ou écrivaine) extrêmement renommé(e), dont les romans sont l’évènement culturel de l’année, se vendant à prix d’or sur le bien connu sinistre marché des occasions. Cette année, vous écrivez un majestueux pavé ayant pour sujet les amours contrariées de Pikachu (hum, dur à porter) et Claudine, deux bambins en crèche à Saint-Ouilles-lès-Oies, sur fond d’odieux trafic de petits pots. Fier parent d’un magnifique fichier texte de plusieurs centaines de milliers de mots, vous posez un regard conquérant sur la page de début du roman… avant de constater avec effroi que vous avez écrit “peaux” à la place de “pots” dans tout le roman.

Il s’agit donc de traquer sans pitié ces pernicieux obstacles à l’obtention du prix Goncourt ! La première chose à laquelle vous pensez est une méthode naïve, que vous faites naturellement sans ordinateur à portée de main, mais qui est à l’origine (avec quelques modifications quand même) de plusieurs algorithmes assez performants (par exemple, celui de Boyer-Moore) : vous écrivez le motif sur une feuille de papier (ou le plus souvent, vous le retenez), puis vous comparez lettre par lettre dans tout le texte, et vous reportez toutes les occurrences du motif dans le texte, c’est-à-dire lorsque vous aurez trouvé une portion de taille m du texte initial qui correspond au motif. C’est faisable si le texte est assez court. Sinon c’est pénible. Et vu que la scène de la première rencontre entre Pikachu et Claudine fait déjà 80 pages, vous vous mettez rapidement à réfléchir à une autre stratégie.

Algorithme de Knuth-Morris-Pratt (1975)

Heureusement Morris et Pratt (et Donald Knuth) viennent à votre rescousse.

Deux définitions importantes (quoique relativement intuitives) avant de commencer : un préfixe de taille j d’un mot M de taille m est le mot M[1,j] tel que j soit inférieur ou égal à m.

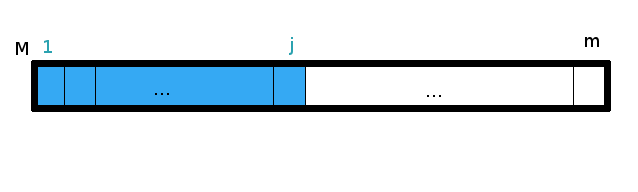
Il est propre si j est strictement inférieur à m.

On définit pareillement un suffixe de taille j de M comme le mot M[j,m] tel que j soit supérieur ou égal à 1.

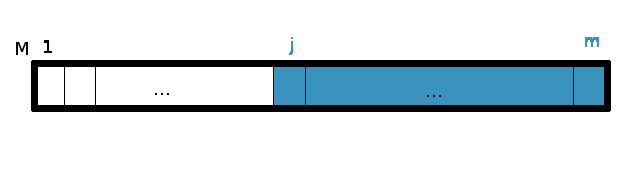
Il est propre si j est strictement supérieur à 1.

T est donc dans notre exemple l’ensemble du roman, et le motif M est égal à “peaux”. L’idée principale de l’algorithme de Morris-Pratt (nous verrons plus tard l’amélioration apportée par Knuth plus tardivement) repose sur la notion de bord maximal. Qu’est-ce qu’un bord en j ? C’est le (plus grand, s’il est maximal) suffixe de T[1,j] qui est également un préfixe de M.

Késako ? Il est temps de faire un dessin d’un bord maximal !

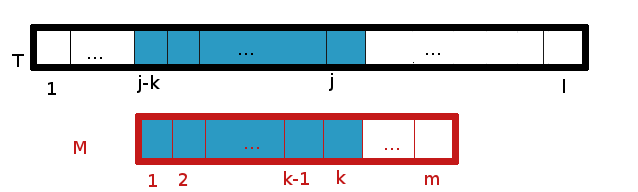
Les lettres alignées de T et de M dont les cases sont en bleu sont les mêmes en T et en M.

On remarquera aisément que si on trouve un bord de longueur m dans T, alors on a trouvé une occurrence de M dans T (car un suffixe de longueur m d’un motif de longueur m n’est autre que le motif lui-même !). Le principe alors de l’algorithme est de regarder à la jième lettre de T la valeur de la longueur du bord le plus grand de T[1,j], pour tout j allant de 1 à l (longueur du texte T). Si c’est m, alors, d’après la remarque précédente, on a gagné.

Et là, vous vous dites (mais si, si) : mais c’est l’algorithme naïf, saupoudré de trois termes techniques assortis d’une notion un peu compliquée ! Cependant, nous avons le moyen de déterminer la longueur d’un bord en fonction des longueurs des bords maximaux précédemment calculés, et c’est cela qui nous sauve. Soit alors la fonction p qui, à la position j de la lettre de T nouvellement lue, associe la longueur du bord maximal de T[1,j]. L’algorithme s’appuie sur deux calculs préliminaires : celui de p pour toute valeur de j, et celui d’un automate très particulier.

Parenthèse automate

Qu’est-ce qu’un automate ici ? Une sorte de machine à plusieurs états qui a pour entrée un mot, qui le lit lettre par lettre, et qui, en fonction de la lettre lue, change, ou pas, d’état.

On distingue parmi les états de la machine :

l’état initial, qui est unique dans les automates que l’on considère ici;
les états finals, qui sont tels que si on arrive à la fin du mot en entrée en se trouvant dans l’un de ces états, la machine s’arrête et renvoie un résultat.

La notion d’état peut paraître très abstraite pour l’instant : un exemple pourra éclaircir tout cela.

L’automate (associé au motif M que l’on recherche) que l’on aura à calculer a des états étiquetés de 0 à m. Cet automate sera tel que, s’il se trouve dans l’état i, alors on aura trouvé au stade j courant de la lecture de T un bord maximal de taille i. Vous l’aurez deviné : l’état initial sera l’état étiqueté 0, l’(unique) état final l’état étiqueté m. Et grâce à la fonction p, on pourra calculer exactement les transitions, c’est-à-dire les passages d’un état à l’autre de l’automate en fonction de la lettre courante lue. Il suffira alors de passer le texte T en entrée d’un tel automate pour retourner les occurrences de M dans T ! (Oui, cela mérite bien un point d’exclamation)

Un exemple, deux exemples d’automates…

Essayons de construire un automate associé au mot “peaux”. Il est vivement conseillé de dessiner l’automate tout en lisant. Nous mettrons par la suite en entrée de l’automate le morceau de texte suivant : “Et là, Pikachu déclara : Tu vas te prendre mes peaux dans la” (que d’intensité dramatique). Normalement, on devrait obtenir une occurrence à la position 36, sans compter ni les espaces ni la ponctuation pour simplifier; les accents ne seront pas pris en compte.

La première lettre que l’on veut rencontrer en cas d’occurrence du motif “peaux” est la lettre p : il en résulte alors que l’on a trouvé un bord de taille maximale 1 (Hé oui, le bord égal à “p”. Yeaaaaaah). On passe alors ainsi de l’état 0 à l’état 1 si on lit p (On n’écrit pas les transitions pour toutes les lettres différentes de p qui font rester dans l’état 0).

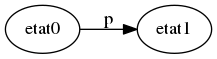
Puis on veut rencontrer la lettre e pour le motif “peaux”. Si c’est le cas, alors on passe à l’état 2; si on lit p, on peut réutiliser cette lettre pour trouver une occurrence de “peaux” (décalée d’une position par rapport à celle que l’on voulait trouver), donc on reste à l’état 1. Sinon on va à l’état 0, puisqu’on ne pourra pas retrouver d’occurrence à partir de la lettre lue.

Si on est déjà à l’état 2, si on lit a, on passe à l’état 3 (par le même raisonnement que précédemment); si on lit la lettre p, par le même raisonnement que précédemment, on retourne à l’état 1; sinon on passe à l’état 0.

On itère le raisonnement pour tout le mot “peaux” : en effet, toutes les lettres de ce mot étant différentes, on ne pourra jamais réutiliser les lettres lues pour retrouver une occurrence, sauf si on lit la lettre p.

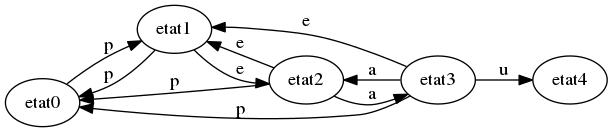
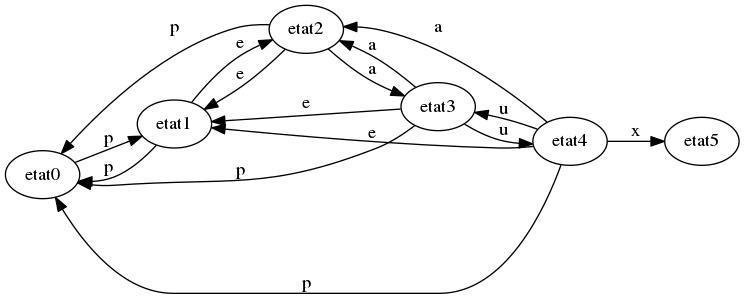
Testons cet automate avec l’entrée “Et là, Pikachu déclara : Tu vas te prendre mes peaux dans la” :

On reste dans l’état 0 jusqu’à la position 5, puis on entre dans l’état 1 à la position 5, puis on revient dans l’état 0. Puis on entre dans l’état 1 à la position 26, puis on revient à l’état 0. Puis à la positon 36, on passe successivement dans l’état 1, puis 2, puis 3, puis 4 et puis 5 : on retourne alors la position 36. Puis on reste dans l’état 0 jusqu’à la fin de l’entrée.

Du mal ? C’est normal. Cet exemple, quoique croustillant, est un peu long. Un exemple plus intéressant (pour nous informaticiens, pas pour le Goncourt) est le motif abbaab sur l’alphabet (a,b) : si vous avez compris l’exemple simple avec “peaux”, vous voyez que l’on passe de l’état 0 à l’état 1 si on lit a, et on reste en 0 sinon.

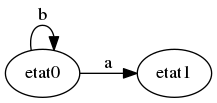
Depuis l’état 1, on passe à l’état 2 si on lit b. Et si on lit a ? On peut réutiliser ce a, car le mot commence par un a. On passe donc à l’état 1.

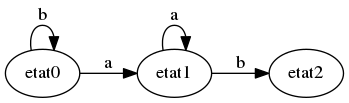
Dans l’état 2, si on lit b, on passe à l’état 3. Sinon, on a donc lu un a; on a alors lu jusques ici le mot …aba. Donc on peut réutiliser le a de la fin pour trouver une éventuelle occurrence du motif. On va donc procéder à un décalage du texte lu, en alignant le premier a de abbaab avec le dernier a de aba, et recommencer la recherche depuis ce a. C’est l’élément clé de l’algorithme, donc accrochez-vous.

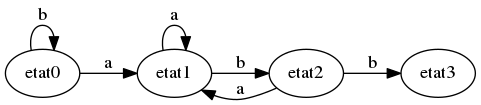
Poursuivons. Dans l’état 3, si on lit a, on passe à l’état 4. Sinon, on a lu le mot …abbb. Ici, la fin du mot que l’on a lu ne peut pas correspondre au motif, qui commence par un a. Donc on est forcé de revenir à l’état 0.

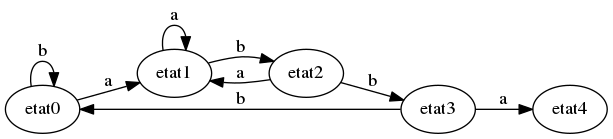
Dans l’état 4, si on lit a, on passe à l’état 5; sinon, on a lu le mot abbab (cela commence à être répétitif, non ?) : le suffixe ab colle avec le début du motif : victoire, on ne rétrograde qu’à l’état 2 !

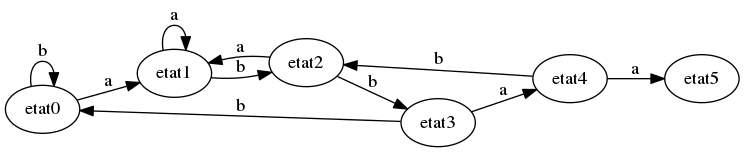
Dans l’état 5, si on lit b, on passe à l’état 6 (et on a trouvé une occurrence du motif !), sinon, on a lu le mot abbaaa. Comme le suffixe a de ce mot correspond à la première lettre du motif, on retourne à l’état 1.

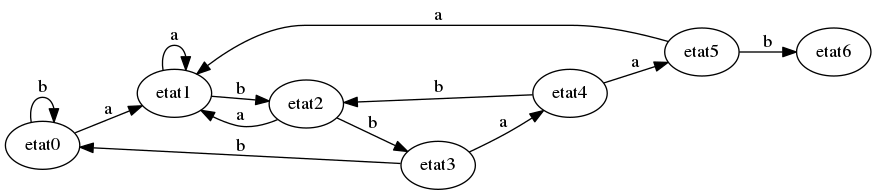
Exercice : testez l’automate précédent avec n’importe quel texte avec que des a ou des b.

Calcul des transitions de l’automate

Pour résumer le calcul des transitions de l’automate :

1) Pour l’état 0, si la lettre que l’on lit n’est pas M[1], alors on reste en 0 en passant à la lettre suivante, sinon on avance dans l’état 1

2) Pour chaque état k différent de m, de manière générale, si on lit M[k], alors on passe à l’état k+1 (on a augmenté la taille du bord maximal de 1) en passant à la lecture de la lettre suivante

3) Pour chaque état k différent de m, si on ne lit pas M[k]… nous allons passer à l’état P[k]. Mais oui, regardez les deux exemples précédents ! Le décalage dont on parlait pour le mot lu revient à ne considérer que le plus grand suffixe du texte lu jusque là qui “colle” avec le début du motif. Autrement dit, le bord maximal du texte lu associé au motif !

4) Pour l’état m, on a trouvé une occurrence du motif dans T; pour la même raison qu’en 3), on démarre ensuite la recherche de l’éventuelle prochaine occurrence à l’état P[m]

L’algorithme, sacrebleu !

On suppose pour l’instant posséder deux fonctions calculP et calculA qui calculent respectivement les valeurs de p pour j allant de 1 à n, et les transitions de l’automate associé à M.

Une transition de l’automate associe, à un état et une lettre lue, l’état dans lequel la machine va se trouver après lecture de la lettre.

On stocke donc les transitions de l’automate dans un tableau à deux entrées : l’une pour les états, l’autre pour toutes les lettres de l’alphabet (En réalité, pour gagner du temps et de l’espace, notamment par rapport à la taille de l’alphabet, l’automate de Morris-Pratt ne comporte que des transitions en cas de lecture de la bonne lettre, et des transitions si on n’a pas lu la bonne lettre, sans répéter la transition pour toute lettre de l’alphabet différente de ladite bonne lettre. Comme le but est de comprendre le principe de l’algorithme, laissons de côté les détails techniques).

L’algorithme est donc :

Stocker dans le tableau automate le résultat de calculA(M) 
(qui à un motif associe son automate)
Stocker dans un tableau de taille n+1 le résultat de calculP(M,T)
Initialiser L la liste des occurrences de M dans T
Initialiser la variable entière etat qui contiendra l'étiquette de l'état courant
Pour toute position j allant de 1 à n faire
       1) etat = automate(etat,T[j])
       2) Si etat = m
            ajouter j à L
Retourner L (tableau des positions)

Ici la terminaison de l’algorithme est évidente (pour peu que l’on soit sûr de la terminaison de calculP et calculA, ce qui est le cas) : on a un nombre de boucles fixé avec la boucle for.

En réalité, calculA consiste seulement à transcrire en langage informatique la construction de l’automate ci-dessus. Maintenant, le plus dur va être de construire (et de comprendre…) la fonction p.

Comment calculer les valeurs de la fonction p efficacement ?

A un j donné, position de lecture dans le texte, on suppose que l’on a trouvé les bords maximaux pour T[1,1], T[1,2], … T[1,j-1].

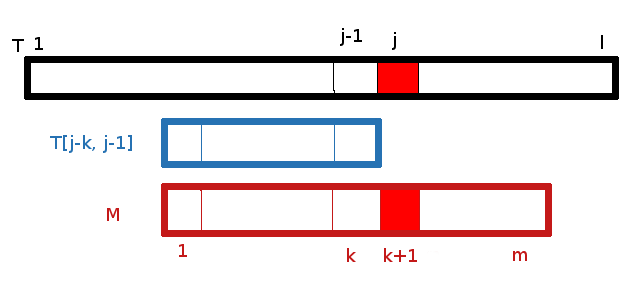
Pour chercher le bord maximal de T[1,j], étant donné le bord maximal de T[1,j-1] (en bleu) :

Si M[k+1] = T[j] (les cases rouges), alors le bord maximal de T[1, j] est alors T[j-k, j] (on peut augmenter par la droite le bord précédent);
Sinon, on ne peut pas trouver de bord maximal de taille supérieure : on retombe sur le bord maximal que l’on avait trouvé pour T[1,k]. Et on itère le raisonnement jusqu’à tomber sur le mot vide, ou sur un bord qui convient. Et là intervient Knuth.

Amélioration de Knuth

La contribution de Knuth à l’algorithme de Morris-Pratt est un raffinement de la fonction p d’origine : p(j) peut avoir comme valeur -1, ce qui signifie que l’on retourne à l’état 0 sans conserver la lettre lue; autrement dit, la longueur du bord maximal du mot T[1,j] est nulle et on sait que l’on ne pourra pas obtenir de bord plus grand en gardant à la prochaine lecture la lettre que l’on a lue. La fonction p est aussi plus facile à calculer : on va pouvoir donner une description plus précise de la fonction calculP. On note P[i] la longueur du bord maximal de T[1, i].

Initialiser un tableau P de taille n+1 à -1
Pour tout i allant de 1 à n faire
    1) initialiser j <- P[i-1]
    2) tant que j est positif et que T[i] 
    est différent de M[j+1] faire j <- P[j] finTant que
    3) P[i] <- j+1

Pour expliquer cet algorithme à l’aspect baroque :

P[0] = -1 car pour le mot vide, le bord maximal est de longueur nulle, en vertu de la remarque précédente.
Puis on part de la longueur du bord maximal pour T[1,i-1] (faire un dessin !), puis on regarde les lettres qui suivent ce bord dans le motif (lettres d’indice supérieur à P[i-1]) : si les lettres dans le texte et dans le motif différent, alors on ne pourra pas trouver de bord plus grand qui convienne : on recherche alors le bord d’avant (étape j <- P[j]) et on itère jusqu’à trouver le bord (sinon, on aura -1).

La terminaison est garantie par le fait que pour un j donné, P[j] < j : en effet, la définition de P[j] nous indique que c’est la longueur d’un suffixe propre de T[1,j]. Un bon exercice pour s’entraîner à la correction est de s’attaquer à cet algorithme.

Si vous avez survécu à tout cela : mes sincères félicitations !

Pour aller plus loin

La notion de bord, ainsi que la fonction p, permettent de structurer rigoureusement la preuve de correction. Elle consiste à montrer que les positions des occurrences du motif, s’ils existent, s’obtiennent par itération de la fonction p. La preuve n’est pas en soi extrêmement dure à comprendre, mais elle est un peu technique (c’est mon avis en tout cas).

Une autre idée d’amélioration a été donnée par Simon, dans l’algorithme qui porte son nom : les transitions revenant à l’état initial sont supprimées, et l’algorithme modifie alors de façon assez subtile les transitions dites arrières (qui vont d’un état à un autre d’étiquette plus petite) pour chaque état non initial. Il en résulte un coût en temps meilleur (si bien implémenté…) que celui de l’algorithme de Knuth-Morris-Pratt. En pratique, un autre algorithme est utilisé, celui de Boyer-Moore : il ne fait pas mieux que KMP dans le pire cas, mais accélère l’obtention du résultat dans les cas favorables -en plus, il est plus simple que KMP.

Enfin, traitons de l’importance des dessins en recherche de motifs. Comme pour les algorithmes de graphes, à moins d’être doté d’une intuition à toute épreuve (et vous obtenez alors mon admiration inconditionnelle), la première étape pour appréhender un algorithme est de faire un dessin, et de le faire tourner sur un petit exemple. Enfin, les dessins sont capitaux pour faire la preuve de correction, et en particulier pour tous les lemmes nécessaires qui, avec un bon dessin, se démontrent pratiquement en un clin d’oeil.