Jouons à Google Flights avec Bellman-Ford !
Contexte
Une deuxième possibilité, outre l’algorithme de Dijkstra, pour résoudre le problème du plus court chemin est l’algorithme de Bellmann-Ford. Celui-ci utilise une méthode de programmation dynamique : découper le problème astucieusement en sous-problèmes plus faciles à résoudre, et retrouver la solution du gros problème en combinant les solutions des plus petits, en sauvegardant les résultats intermédiaires dans un tableau -voir l’article sur le rendu de monnaie. Et, pour cela, trouver un cas dit de base, où on pourra répondre facilement au problème, puis une relation de récurrence reliant les solutions de certains sous-problèmes pour donner la solution d’un problème plus gros.
On cherche donc le plus court chemin dans une carte entre deux points A et B. L’un des intérêts de cet algorithme, contrairement à l’algorithme de Dijkstra, est qu’il ne se formalise pas de la présence de chemins de coûts négatifs dans la carte.
Mais le graphe ne doit pas comporter de cycles de coût total strictement négatif : autrement dit, il n’existe pas trois points A, B, et C tels que l’on puisse aller de A à B, de B à C et de C à B, et tels que la somme des coûts sur chacun de ces trois arcs soit strictement négative. L’exemple ci-dessous comporte un tel cycle :
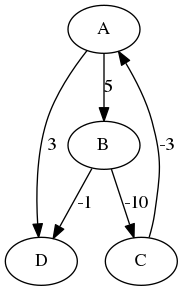
Voir la première section de l’article sur l’algorithme de Dijkstra pour une description des graphes en informatique.
Un exemple concret : Google Flights
Prenons un cas où le coût n’est non pas le temps de transport, mais le prix du voyage. Cherchant un lieu de villégiature pour pouvoir faire tourner vos algorithmes en paix, vous cherchez les prix les plus intéressants pour un voyage en avion vers l’Antarctique (si, si, votre ordinateur va adorer le climat). Si vous avez l’expérience des recherches de billets d’avion sur Internet, vous savez bien qu’un trajet direct Paris-Terre Adélie n’est pas toujours le moins cher, et que les deux trajets Paris-Tombouctou puis Tombouctou-Terre Adélie peuvent à eux deux être plus économiques. Résumons : vous cherchez par conséquent un plus court chemin, donc ici le moins cher, entre Paris et Terre Adélie, dans la carte comportant tous les trajets d’avion possibles à cette période de l’année, où les points reliés sont les différents aéroports.
Une première méthode serait de parcourir méthodiquement tous les trajets possibles de Paris à Terre Adélie, avec toutes les escales imaginables (sans boucle, bien sûr), puis de comparer les coûts totaux de tous ces trajets et sélectionner celui de coût minimal. Vous n’avez pas envie de faire ce boulot ? L’ordinateur non plus, et ici intervient l’algorithme de Bellman-Ford.
Algorithme de Bellman-Ford (1956)
Prenons une carte simplifiée des transports internationaux en avion, en l’an de grâce 2017 : soit P (Paris), L (Londres), T (Tombouctou), B (Beyrouth), Z (Zagreb) et A (Terre Adélie). Petit rappel sur les graphes : les points P, L, T, B, Z, et A sont les noeuds du graphe, et les flèches les reliant sont appelées arcs. On ne dessine pas les arcs qui vont d’un noeud à lui-même, qui sont de coût 0 ici.
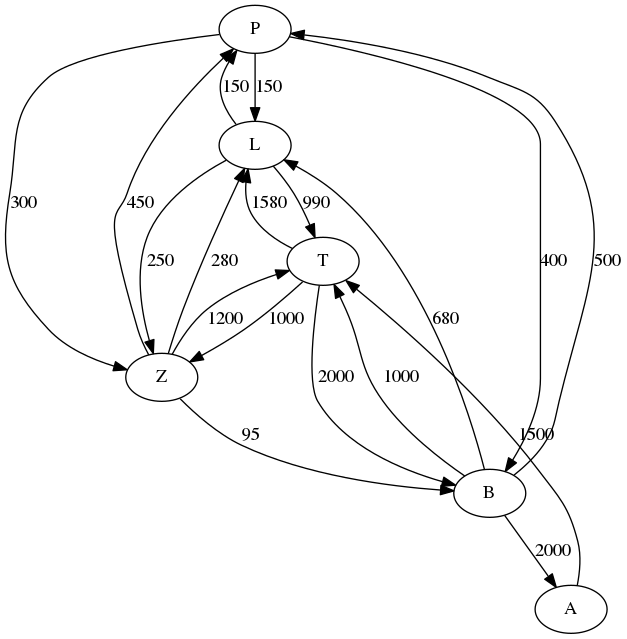
Vous pouvez constater que ce que j’appelle “coût” (l’addition de tous les nombres étiquetant les arcs du chemin), et “longueur” d’un chemin entre deux points (c’est-à-dire le nombre d’arcs entre ces deux points) sont bien deux choses différentes. Désormais, quand je parlerai de plus court chemin, je penserai au chemin le moins coûteux, pas celui qui comporte le moins d’arcs.
Comme pour le problème de rendu de monnaie, on peut se ramener au problème de trouver le coût du plus court chemin de P à A, puis en déduire l’ordre des noeuds à suivre.
Quel sous-problème serait alors le plus intéressant pour le problème de trouver le coût du plus court chemin de P à A ? Quelle quantité choisir, que l’on pourrait faire décroître facilement pour obtenir un sous-problème ? Supposons que l’on prenne le nombre maximal d’arcs à utiliser entre deux points, que l’on note n (ce qui est le plus naturel). L’idée serait de fixer le point de départ P, et, comme dans l’algorithme de Dijkstra, progresser noeud à noeud en partant de P, et donc découper astucieusement le chemin de P à A en sous-chemins. Le problème (X, n) alors considéré est trouver le coût du plus court chemin de longueur inférieure à n de P à X.
Etudions le cas de base : pour n = 0, on ne peut accéder qu’au point de départ P, et le coût nécessaire est le coût étiquetant l’arête allant de P à P (dans notre exemple de vol aérien, ce nombre vaut 0 en général), et pour tout noeud X différent de P, on fixe un coût infini : il n’existe pas de plus court chemin, car il n’existe pas de chemin tout court.
Donc la liste des coûts correspondant à n = 0 vaut :
X = P, L, T, B, Z, A
Coût = 0, +Inf, +Inf, +Inf, +Inf, +Inf
Pour n = 1, on ne peut accéder qu’aux noeuds X voisins de P, c’est-à-dire aux points reliés directement à P par une seule arête. Si les noeuds P et X ne sont pas voisins (peuchère), le coût du plus court chemin de longueur inférieure ou égale à 1 entre les deux est infini. Sinon, ce coût vaut le nombre étiquetant l’arc entre P et le voisin X considéré. On peut voir ce chemin de longueur 1 comme un plus court chemin entre P et Y, plus un chemin de Y à X, où Y est un voisin de X. Si X et P sont voisins, Y = P, et le coût de ce chemin vaut 0 + coût sur l’arc entre P et X. Sinon, le coût de ce chemin vaut infini + un nombre potentiellement infini, donc est de coût infini. La ligne n = 1 est donc :
X = P, L, T, B, Z, A
Coût = 0, 150, +Inf, 400, 300, +Inf
On commence à voir comment découper le chemin en sous-problèmes. Mais faisons le cas n = 2 pour se faire une idée plus précise. S’il n’y a pas de chemin, alors X est différent de P, X et P ne sont pas voisins, et X et P n’ont aucun voisin en commun : le coût retourné pour ce problème est donc infini, d’après les cas précédents.
S’il existe un chemin, on sait donc que l’on a au maximum un autre noeud Y, différent de P et de X, entre P et X. Si P = X, ou si P et X sont voisins, on tombe sur les cas précédents. Sinon, il existe un noeud Y différent de P et de X sur le chemin recherché, et ce noeud est donc forcément un voisin de X, puisqu’à distance strictement inférieure à 2 de P et X, et que Y est différent de P et de X. Le chemin final entre P et X est composé donc de l’arc Y-X, et du plus court chemin de P à Y de longueur inférieure à 2-1=1 (notre sous-problème (Y, 1)).
X = P, L, T, B, Z, A
Coût = 0, 150, 990 + 150, 400, 300, 2 000 + 400
Mais quel voisin choisir ? Intuitivement, on aimerait faire les plus petits trajets possibles entre voisins. Donc pourquoi ne pas prendre le voisin Y à partir duquel on peut accéder à X avec un coût minimal ? Mais l’intuition est ici mauvaise (hé oui). Imaginez si pour aller de Paris à Terre Adélie, vous avez à disposition un vol de Paris à Kinshasa à 50 euros, un vol de Paris à Beyrouth à 400 euros, puis un vol de Kinshasa à Terre Adélie à 1 000 euros et un vol de Beyrouth à Terre Adélie à 600 euros (c’est un maigre éventail de possibilités, certes). Le point le plus proche de Paris (au niveau du prix…) est Kinshasa, cependant votre voyage en passant par Kinshasa vaudra 50 + 1 000 = 1 050 euros, contre 400 + 600 = 1 000 euros en passant par Beyrouth. Ici, la stratégie gloutonne ne fonctionne pas. Il va donc falloir parcourir tous les voisins de X, et, pour le coût du problème (X, n), choisir un voisin Y qui minimise la quantité (coût de l’arc Y-X + coût optimal pour le problème (Y, n-1)).
Enfin, sur quel problème lancer l’algorithme ? On cherche un majorant de la longueur du plus court chemin (c’est-à-dire, un nombre qui sera toujours supérieur à la longueur d’un plus court chemin entre deux noeuds quelconques du graphe). Un majorant direct est bien sûr le nombre d’arcs dans le graphe, qui est lui-même toujours plus petit que le nombre maximal d’arcs qui peut exister dans un graphe avec un nombre fixé de noeuds n, où il n’y a qu’un arc au maximum entre deux noeuds : n x n (chaque noeud est relié à tous les autres noeuds dans le graphe, y compris lui-même). Mais il y a plus astucieux.
Imaginez que, de façon absurde, le plus court chemin entre P et A dans le graphe à n noeuds soit de longueur m supérieure ou égale à n. Alors le chemin passe forcément au moins deux fois dans l’un des noeuds. Pour vous convaincre, prenez un chemin de longueur m : x1, x2, …, xm (liste des arcs, qui ne comprend pas d’arc allant d’un noeud à lui-même), et associez chaque arc au noeud duquel il sort. Vous obtenez une liste de m noeuds + le point d’arrivée, donc m+1 noeuds. Or vous n’avez que n noeuds à disposition, et n est strictement inférieur à m+1. Donc il existe au moins un noeud Z qui est répété au moins deux fois.
Découpons le chemin précédent en trois parties : le chemin allant de P à la première apparition de Z, le chemin de Z retournant en Z (qui est de longueur non nulle car on n’a pas autorisé les arcs allant d’un noeud à lui-même), et le chemin allant de Z jusqu’à A.
Supprimons la deuxième partie du chemin. On obtient un autre chemin de P à A, de longueur strictement inférieure à m. Est-il plus court au sens moins coûteux ? Le coût total du chemin est la somme des trois parties que l’on a découpées. Si la partie qui boucle sur Z est de coût total positif ou nul, alors le chemin obtenu en supprimant cette partie est bien plus court. En revanche, si la partie qui boucle sur Z est de coût total strictement négatif, c’est faux. Il faut donc supposer que le graphe ne possède pas de cycle de coût total strictement négatif.
Si on accepte cette condition, on obtient un chemin de P à A, strictement plus court que le plus court chemin que l’on avait trouvé. Cela n’a pas de sens ? C’est normal, il y a une contradiction. Cela signifie que l’une des deux hypothèses que l’on a faites est fausse. Si le graphe possède un cycle de coût total strictement négatif, alors le plus court chemin entre P et A est un chemin de longueur infinie, contenant une infinité de fois le cycle de coût total strictement négatif. Sinon, l’hypothèse que l’on a faite au début, que le plus court chemin entre P et A puisse être de longueur supérieure à n, est fausse.
Conclusion : on peut majorer la longueur du plus court chemin par le minimum entre le nombre d’arcs et n-1, où n est le nombre de noeuds dans le graphe ne contenant de cycle de coût total strictement négatif. Et on peut appeler l’algorithme sur le problème (A, n-1).
Résumons l’algorithme (M[i, j] correspond à la case à la ligne i et à la colonne j de la matrice M) :
Initialiser une matrice M indexée sur les lignes par 0, 1, ..., n-1, et sur les colonnes par les noeuds du graphe
Initialiser le cas n=0 : sur la ligne 0, écrire M[0, X] = +infini pour x différent de P, écrire M[0, P] = 0
Pour l allant de 1 à n-1
Pour tout noeud v du graphe (dans n'importe quel ordre)
Chercher le voisin w de v qui minimise la quantité (coût de l'arc w-v + M[l-1, w]) (M[l-1, w] est le coût du sous-problème (w, l-1))
Ecrire M[l, v] = coût de l'arc w-v + M[l-1, w]
Fin pour
Fin pour
Retourner M[n-1, A]A l’étape l, M[x, Y], avec x un entier strictement inférieur à l, et Y un noeud quelconque, est toujours déjà calculé, parce que l a des valeurs croissantes.
L’algorithme termine car il y a au maximum (n-1) x n x (n-1) boucles exécutées par l’algorithme : la première correspondant à la boucle sur l, la deuxième au parcours des noeuds du graphe, et la dernière à la recherche d’un voisin (chaque noeud ayant au maximum n-1 voisins différents de lui-même dans un graphe à n noeuds).
Exemples
Vous n’avez rien compris ? C’est parfaitement normal. Et c’est à cela que servent les dessins (et les exemples) !
Exercice : appliquer l’algorithme précédent à notre carte, que je rappelle ici :

Au début, il faut initialiser la matrice M à 6 lignes, et 6 colonnes :
P, L, T, B, Z, A 0, +Inf, +Inf, +Inf, +Inf, +Inf (n = 0) NA, NA, NA, NA, NA, NA (n = 1) NA, NA, NA, NA, NA, NA (n = 2) NA, NA, NA, NA, NA, NA (n = 3) NA, NA, NA, NA, NA, NA (n = 4) NA, NA, NA, NA, NA, NA (n = 5 = 6 - 1)
Pour aller plus loin
La preuve de correction en programmation dynamique suit toujours le même schéma : vérifier que la solution trouvée pour le ou les cas de base est optimale, et montrer que la solution obtenue par utilisation de la relation de récurrence reste optimale, par exemple en montrant que toute autre solution a un coût au moins égal à celui de la solution trouvée par l’algorithme. C’est donc un peu comme une récurrence sur les paramètres du problème.
L’exemple considéré ici ne permet pas de souligner que l’algorithme de Bellman-Ford peut retourner le bon résultat même s’il existe des arcs de coût strictement négatif. Mais la démonstration faite précédemment s’applique également s’il existe des arcs de coût négatif.
En revanche, l’algorithme de Bellman-Ford ne permet pas de repérer les boucles de coût total strictement négatif, et ne retourne pas le bon résultat dans le cas où il existe un tel cycle, pour la raison citée précédemment.
Par contre, l’algorithme de Floyd-Warshall, qui permet aussi de trouver le plus court chemin dans un graphe, peut les détecter.