Path Statistics
In this article, I talk about this problem (of HackerRank). Try to solve it first!
You are given a tree with $n$ nodes, that is, an acyclic connected graph, where each node $i$ is assigned a value $c_i$.
You must answer $q$ queries in the form
u v k. For each query, find and print the $k^{th}$ most frequent value on the path between $u$ and $v$. If two values appear the same number of times, for tie-breaking, the smaller number is considered less frequent than, the bigger one.Constraints: $n, q ≤ 5 * 10^4$
From trees to arrays
Any problem about shortest paths in a tree should ring a bell: you can probably solve a related problem on an array, and generally it is easier to work with arrays.
Depending on the problem, you want to do an Eulerian circuit (DFS and log all the vertices you see) or an Eulerian tour (DFS and log only the first and last occurence of each vertex). I am not sure of the names here, it is just to state that there is a broad range of techniques based on writing down edges or vertices during a DFS.
For example, there is a classical reduction from LCA to RMQ (see on topcoder.com) that uses Eulerian circuit.
But here, we are going to use an Eulerian tour:
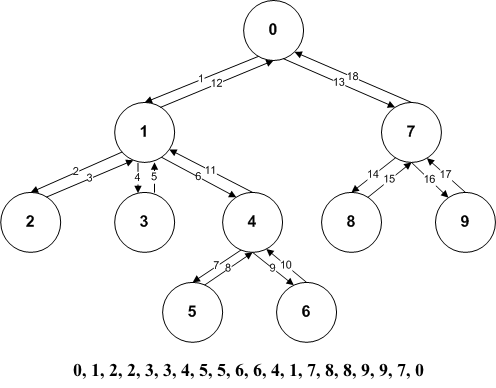
Each vertex $v$ appears two times, let’s note them $ST(v)$ and $EN(v)$.
The nodes between $ST(v)$ and $EN(v)$ are exactly the descendants of $v$.
We are interested in computing on the path between two nodes $u$ and $v$ with $ST(u) ≤ ST(v)$.
The path has two parts: going up to $LCA(u, v)$ and going down. When you go up, you write a $ST$ and when you go down you write an $EN$.
Since you start from $u$, you already passed all the $ST$ of the ancestors of $u$. Since you arrive to $v$, you did not see any $EN$ of its ancestors.
Thus, when you traverse $[EN(u), ST(v)]$, you see one time each vertex on $ u \rightarrow v$ except $LCA(u, v)$. The vertices in $[EN(u), ST(v)]$ that are not on $u \rightarrow v$ appear twice because their subtree has no intersection with the path.
In conclusion:
- If $LCA(u, v) = u$ then you traverse $[ST(u), ST(v)]$ without the duplications.
- Else, you traverse $[EN(u), ST(v)]$ without the duplications and add $ST(P)$.
We can now express any query on the tree as a range query on the Eulerian tour. Note that you also have to compute the LCA.
You can find more about this technique and the next one on codeforces.com.
MO’s algorithm
The reduction we found is not useful for a small number of queries because it makes each query in $O(n)$, and is slightly slower than just computing the path because of the vertices that appear twice: you have to traverse them and use a boolean array to remember them.
In this part, $n$ is the size of the array that was $2n$ in the previous part.
We are going to prove:
If you have to answer $Q$ range queries that can be updated in $O(T)$ on an array of size $n$, you can solve them in $O(Q \log Q + (n + Q)\sqrt n \times T)$.
Let’s note the queries $[a, b]$. “that can be updated” means you can compute the program state associated with $[a±1, b]$ or $[a, b±1]$ from the program state associated with $[a, b]$.
We can already compute all the possible queries in $O(T n^2)$ by looping on $a$ and $b$.
MO’s algorithm is just a reordering of the queries.
We divide the array in $\sqrt n$ blocks of size $\sqrt n$ and sort $[a, b]$ like $\left (\left\lfloor \frac{a}{\sqrt n} \right\rfloor, b\right )$. $\left\lfloor \frac{a}{\sqrt n} \right\rfloor$ is the index of the block $a$ belongs to.
While handling the queries, $b$ changes at most $n$ times per block, so at most $n \sqrt n$ times.
If $a$ stays in the same block, $a$ cannot change by more than $\sqrt n$ ; and the number of all “block change” steps is less than $n$, so $a$ changes at most $Q\sqrt n + n$ times.
Summing the two gives $O((n + Q)\sqrt n)$ steps so an overall complexity $O(Q \log Q + (n + Q)\sqrt n \times T)$ (because of the sort).
A first solution
We have now reduced the problem to:
Read a vertex $v$.
If $v$ is in the current set of vertices, remove it.
Else add it.
Return the $k^{th}$ most frequent value in the set.
When we read $v$, we retrieve $c_v$ from the array given as input.
Then we use a mapping $freq$ to get $freq[c_v]$ from $c_v$.
Finally, we use a sorted set that contains $(freq[c_v], c_v)$ for each value $c$ to solve the $k^{th}$ problem in $O(\log n)$.
The sorted set can be implemented easily using Skip Lists: https://github.com/jilljenn/tryalgo/pull/34.
Here, $T = O(\log n)$ so the complexity is $O((n + Q)\sqrt n \log n)$.
Unfortunately, when I did this in Python during the contest, the constant hidden in the skip lists was too big, and I got less tests than with a naive method.
The $O((n+ Q)\sqrt n)$ solution
What is interesting is that in the previous solution the update and the queries were done in $O(\log n)$. There is a “hidden” $O(Q \log n)$ at query time.
To achieve $O((n+ Q)\sqrt n)$, we need to the updates in $O(1)$, but we can afford a $O(\sqrt n)$ query.
The important part is that we are working on frequencies that sum up to $n$.
We also suppose the values are contiguous, that is $freq$ is now an array.
The data structure
We use a boolean array $A$ of size $n$, but the interesting part is not the values but the indexes.
We maintain $A[index[v][f]] = true$ if $freq[v] = f$ else $false$.
We define the order of $index$ to be exactly the same as the order requested by the problem: frequencies then values. Note that it is $index[v][f] $ and not $index[f][v]$: the total size of $index$ is exactly $n$.
For example, if the total frequencies are ${1: 2, 4: 3, 5: 1}$, $index = {1: [0, 3], 4: [1, 4, 5], 5: [2]}$.
We also use the square root decomposition (more on infoarena.com) of $A$: $A^*[i] = sum(A[i \sqrt n: (i+1)\sqrt n])$.
Update algorithm in $O(1)$
Let’s say we read the value (not the vertex) $v$ and $f := freq[v]$.
We just need to update $A[index[v][f]]$, and $A^*[index[v][f] // \sqrt n]$, in $O(1)$.
Query algorithm in $O(\sqrt n)$
It is the classic square root decomposition query algorithm in $O(\sqrt n)$: search in $A^*$ (steps of $\sqrt n$) then in $A$ (steps of $1$) until you find the first index of $A$ with cumulative sum $k$.
You can then use the inverse array of $index$ to retrieve the associated $v$ and $f$ values (even if you only need $v$).
Conclusion
This is a complex problem that required a lot of different algorithms!
We saw:
- how to transform a tree problem into an array problem using Eulerian tour and LCA,
- MO’s algorithm to sort range queries on an array,
- a general data structure for $k^{th}$ most frequent value updates and queries in $O(\log n)$: skip lists,
- a custom data structure for $k^{th}$ most frequent value queries in a bounded set with updates in $O(1)$ and queries in $O(\sqrt n)$.